题目内容
18.已知数列{an}满足a1=3,an+1=$\frac{3n-1}{3n+2}$an(n≥1),求an的通项公式.分析 数列{an}满足a1=3,an+1=$\frac{3n-1}{3n+2}$an(n≥1),可得$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{3n-4}{3n-1}$(n≥2),利用“累乘求积”即可得出.
解答 解:∵数列{an}满足a1=3,an+1=$\frac{3n-1}{3n+2}$an(n≥1),
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{3n-4}{3n-1}$(n≥2),
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$$•\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{3}}{{a}_{2}}$•$\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$
=$\frac{3n-4}{3n-1}$•$\frac{3n-7}{3n-4}$•…•$\frac{5}{8}$•$\frac{2}{5}$•3
=$\frac{6}{3n-1}$,当n=1时也成立.
∴an=$\frac{6}{3n-1}$.
点评 本题考查了递推关系、“累乘求积”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知奇函数f(x)=ax3+bx2+2x+c,且f(1)=5,则f(2)=( )
| A. | -5 | B. | 10 | C. | 25 | D. | 28 |
13.已知x>0,y>0,xy-x-2y+$\frac{3}{2}$=0,则x+2y的取值范围是( )
| A. | (0,2]∪[6,+∞) | B. | (0,$\frac{3}{2}$]∪[6,+∞) | C. | ($\frac{3}{2}$,2]∪[6,+∞) | D. | [6,+∞) |
3.某四棱锥的三视图如图所示,该四棱锥外接球的表面积为( )
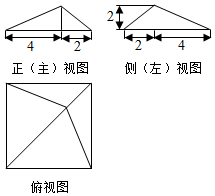

| A. | 72π | B. | 100π | C. | 108π | D. | 72$\sqrt{2}π$ |
7.函数f(x)=-x2+3x-a,g(x)=2x-x2,若f[g(x)]≥0对x∈[0,1]恒成立,则实数a的范围是( )
| A. | (-∞,2] | B. | (-∞,e] | C. | (-∞,ln2] | D. | [0,$\frac{1}{2}$) |
 如图,设正棱锥S-ABC的体积为6,E,F和G分别是SA、AB和BC的中点,已知二面角E-FG-A的平面角为60°,求SA.
如图,设正棱锥S-ABC的体积为6,E,F和G分别是SA、AB和BC的中点,已知二面角E-FG-A的平面角为60°,求SA.