题目内容

11．三棱锥S-ABC中，SA⊥面ABC，△ABC为等边三角形，SA=2，AB=3，则三棱锥S-ABC的外接球的表面积为16π．

分析 由已知结合三棱锥和正三棱柱的几何特征，可得此三棱锥外接球，即为以△ABC为底面以SA为高的正三棱柱的外接球，分别求出棱锥底面半径r，和球心距d，得球的半径R，然后求解表面积．

解答 解：根据已知中底面△ABC是边长为3的正三角形，SA⊥平面ABC，SA=2，
可得此三棱锥外接球，即为以△ABC为底面以SA为高的正三棱柱的外接球，
∵△ABC是边长为3的正三角形，
∴△ABC的外接圆半径r=$\sqrt{3}$，球心到△ABC的外接圆圆心的距离d=1，
故球的半径R=$\sqrt{3+1}$=2．
三棱锥S-ABC外接球的表面积为：4π×4=16π．
故答案为：16π．

点评 本题考查的知识点是球内接多面体，熟练掌握球的半径R公式是解答的关键．

练习册系列答案
相关题目
1．设不等式组$\left\{\begin{array}{l}{x+2y-5≤0}\\{x≥-1}\\{y≥0}\end{array}\right.$，表示的平面区域为D，点A（3，0），原点O（0，0），在区域D内随机取一点M，则点M满足|MA|≥2|MO|的概率是（　　）
A．$\frac{2π}{9}$B．$\frac{π}{6}$C．$\frac{π}{9}$D．$\frac{π}{12}$
2．方程（x+y）$\sqrt{{x}^{2}+{y}^{2}-4}$=0表示的曲线是两条射线和一个圆．
19．求与直线5x+3y-1=0垂直，且在两坐标轴上的截距之和为4的直线方程．
6．设f（x）=ex-1，当x＞-1时，证明：f（x）＞$\frac{2{x}^{2}+x-1}{x+1}$．
16．对于非零向量$\overrightarrow{a}$，$\overrightarrow{b}$下列5个命题正确的个数是（　　）
（1）若$\overrightarrow{a}$，$\overrightarrow{b}$共线，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|；
（2）若$\overrightarrow{a}$，$\overrightarrow{b}$不共线，则|$\overrightarrow{a}$+$\overrightarrow{b}$|＜|$\overrightarrow{a}$|+|$\overrightarrow{b}$|；
（3）若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|，则$\overrightarrow{a}$+$\overrightarrow{b}$同向；
（4）若|$\overrightarrow{a}$+$\overrightarrow{b}$|＜|$\overrightarrow{a}$|+|$\overrightarrow{b}$|，则$\overrightarrow{a}$，$\overrightarrow{b}$不共线；
（5）||$\overrightarrow{a}$|-|$\overrightarrow{b}$||≤|$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|
A．1B．2C．3D．4
3．某四棱锥的三视图如图所示，该四棱锥外接球的表面积为（　　）
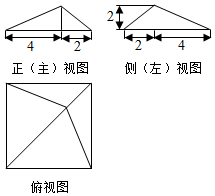
A．72πB．100πC．108πD．72$\sqrt{2}π$
20．已知点P是抛物线x2=4y上的动点，点P在x轴上的射影是Q，点A（8，7），则|PA|+|PQ|的最小值为（　　）
A．7B．8C．9D．10
3．点（5，-3）到直线x+2=0的距离等于（　　）
A．7B．5C．3D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网