题目内容
根据要求,求x的取值范围:
(1)tan
≥
;
(2)cot2x≤-
;
(3)|sinx|≤|cosx|;
(4)logxtanx>0;
(5)log
sin
-log
cos
>-1且-2π<x<2π.
(1)tan
| x |
| 2 |
| 3 |
(2)cot2x≤-
| 3 |
(3)|sinx|≤|cosx|;
(4)logxtanx>0;
(5)log
| 3 |
| x |
| 2 |
| 3 |
| x |
| 2 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:由条件利用对应的三角函数的图象和性质,求出三角不等式的解集.
解答:
解:(1)由tan
≥
,可得kπ+
≤
<kπ+
,k∈z,求得 2kπ+
≤x<2kπ+π,k∈z,即要求的x的范围为{x|2kπ+
≤x<2kπ+π,k∈z }.
(2)由cot2x≤-
,可得-
≤tanx<0,可得kπ-
≤x<kπ+0,k∈z,即要求的x的范围为{x|kπ-
≤x<kπ+0,k∈z}.
(3)由|sinx|≤|cosx|,可得 cos2x-sin2x≥0,cos2x≥0,可得 2kπ-
≤2x≤2kπ+
,k∈z,
求得 kπ-
≤x≤kπ+
,k∈z,即要求的x的范围为{x|kπ-
≤x≤kπ+
,k∈z}.
(4)由 logxtanx>0,可得
①,或
②.
解①求得 kπ+
<x<kπ+
,k∈z,且k≥0.解②求得 0<x<
.
综上可得,即要求的x的范围为{x|kπ+
<x<kπ+
,k∈z,且k≥0;或 0<x<
}.
(5)由log
sin
-log
cos
>-1,可得log
(tan
)>-1,故有 tan
>-
,解得 kπ-
<
<kπ+
,k∈z,
即 2kπ-
<x<2kπ+π.再结合-2π<x<2π,可得-
<x<π,即即要求的x的范围为(-
,π).
| x |
| 2 |
| 3 |
| π |
| 3 |
| x |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
(2)由cot2x≤-
| 3 |
| ||
| 3 |
| π |
| 6 |
| π |
| 6 |
(3)由|sinx|≤|cosx|,可得 cos2x-sin2x≥0,cos2x≥0,可得 2kπ-
| π |
| 2 |
| π |
| 2 |
求得 kπ-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
(4)由 logxtanx>0,可得
|
|
解①求得 kπ+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
综上可得,即要求的x的范围为{x|kπ+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
(5)由log
| 3 |
| x |
| 2 |
| 3 |
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
| 3 |
| π |
| 3 |
| x |
| 2 |
| π |
| 2 |
即 2kπ-
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
点评:本题主要考查三角函数的图象特征,三角不等式的解法,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=(x-a)2+(
-a)2-a2+2(x>0,a∈R),若函数f(x)有四个不同的零点,则a的取值范围是( )
| 2 |
| x |
A、-3
| ||||
B、a>3
| ||||
C、2
| ||||
D、a>2
|
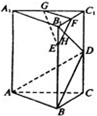 如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H.
如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H. 如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.