题目内容
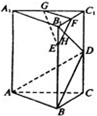 如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H.
如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H.(Ⅰ)求证:B1D⊥平面ABD;
(Ⅱ)求证:平面EFG∥平面ABD;
(Ⅲ)求平面EG与平面ABD的距离.
考点:平面与平面平行的判定,直线与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件得AB⊥平面BB1C1C,从而AB⊥B1D,又B1D⊥BD,由此能证明B1D⊥平面ABD.
(Ⅱ)由已知条件推导出EF∥平面ABD,GF∥平面ABD,由此能证明平面EFG∥平面ABD.
(Ⅲ)由已知条件推导出HD为平行平面EFG与ABD之间的距离,由此能求出结果.
(Ⅱ)由已知条件推导出EF∥平面ABD,GF∥平面ABD,由此能证明平面EFG∥平面ABD.
(Ⅲ)由已知条件推导出HD为平行平面EFG与ABD之间的距离,由此能求出结果.
解答:
(Ⅰ)证明:由直三棱柱的性质,得平面ABC⊥平面BB1C1C,
又AB⊥BC,∴AB⊥平面BB1C1C,
又B1D?平面BB1C1C,
∴AB⊥B1D,
∵BC=CD=DC1=B1C1=2,
∴在Rt△BCD和Rt△DC1B1中,
∠BDC=∠B1DC1=45°,
∴∠BDB1=90°,即B1D⊥BD,
又AB∩BD=B,
∴B1D⊥平面ABD.
(Ⅱ)证明:由题意知EB1=B1F=1,
∴在Rt△EB1F中,∠FEB1=45°,
又∠DBB1=45°,∴EF∥BD,
∵BD?平面ABD,EF不包含于平面ABD,
∴EF∥平面ABD,
∵G、F分别为A1C1、B1C1的中点,
∴GF∥A1B1,又A1B1∥AB,
∴GF∥AB,
∵AB?平面,GF不包含平面ABD,
∴GF∥平面ABD,
∵EF?平面EFG,GF?平面EFG,EF∩GF=F,
∴平面EFG∥平面ABD.
(Ⅲ)解:∵B1D⊥平面ABD,平面EGF∥平面ABD,
∴B1D⊥平面EGF,
∴HD为平行平面EFG与ABD之间的距离,
∴HD=B1D-B1H=2
-
=
.
又AB⊥BC,∴AB⊥平面BB1C1C,
又B1D?平面BB1C1C,
∴AB⊥B1D,
∵BC=CD=DC1=B1C1=2,
∴在Rt△BCD和Rt△DC1B1中,
∠BDC=∠B1DC1=45°,
∴∠BDB1=90°,即B1D⊥BD,
又AB∩BD=B,
∴B1D⊥平面ABD.
(Ⅱ)证明:由题意知EB1=B1F=1,
∴在Rt△EB1F中,∠FEB1=45°,
又∠DBB1=45°,∴EF∥BD,
∵BD?平面ABD,EF不包含于平面ABD,
∴EF∥平面ABD,
∵G、F分别为A1C1、B1C1的中点,
∴GF∥A1B1,又A1B1∥AB,
∴GF∥AB,
∵AB?平面,GF不包含平面ABD,
∴GF∥平面ABD,
∵EF?平面EFG,GF?平面EFG,EF∩GF=F,
∴平面EFG∥平面ABD.
(Ⅲ)解:∵B1D⊥平面ABD,平面EGF∥平面ABD,
∴B1D⊥平面EGF,
∴HD为平行平面EFG与ABD之间的距离,
∴HD=B1D-B1H=2
| 2 |
| ||
| 2 |
3
| ||
| 2 |
点评:本题考查直线与平面垂直的证明,考查平面与平面平行的证明,考查两平行平面间的距离的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若向量
,
是一组基底,向量
=x
+y
(x,y∈R),则称(x,y)为向量
在基底
,
下的坐标.现已知向量
在基底
=(1,2),
=(-1,1)下的坐标为(-1,-3),则向量
在另一组基底
=(1,-1),
=(0,-1)下的坐标为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| t |
| p |
| q |
| t |
| m |
| n |
| A、(-1,-3) |
| B、(2,-3) |
| C、(2,-5) |
| D、(2,3) |
 如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2