题目内容
已知向量
=（1，-2），
=（4，-1），
=（m，m+1）．
（1）若
∥
，求实数m的值；
（2）若△ABC为直角三角形，求实数m的值．
| OA |
| OB |
| OC |
（1）若
| AB |
| OC |
（2）若△ABC为直角三角形，求实数m的值．
考点：平面向量数量积的运算,平面向量共线（平行）的坐标表示,数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：（1）通过
∥
，利用平行的充要条件，列出关系式即可求实数m的值；
（2）利用三角形的直角的可能性，通过向量的数量积为0，求实数m的值．
| AB |
| OC |
（2）利用三角形的直角的可能性，通过向量的数量积为0，求实数m的值．
解答：
解：（1）因为向量
=(1，-2)，
=(4，-1)，
所以
=
-
=(3，1)．
因为
∥
，且
=(m，m+1)，
所以3（m+1）-m=0．
所以m=-
．
（2）由（1）可知，
=
-
=(3，1)，
=
-
=(m-1，m+3)，
=
-
=(m-4，m+2)．
因为△ABC为直角三角形，所以
⊥
，
⊥
或
⊥
．
当
⊥
时，有3（m-1）+m+3=0，解得m=0；
当
⊥
时，有3（m-4）+m+2=0，解得m=
；
当
⊥
时，有（m-1）（m-4）+（m+3）（m+2）=0，解得m∈∅．
所以实数m的值为0或
．
| OA |
| OB |
所以
| AB |
| OB |
| OA |
因为
| AB |
| OC |
| OC |
所以3（m+1）-m=0．
所以m=-
| 3 |
| 2 |
（2）由（1）可知，
| AB |
| OB |
| OA |
| AC |
| OC |
| OA |
| BC |
| OC |
| OB |
因为△ABC为直角三角形，所以
| AB |
| AC |
| AB |
| BC |
| AC |
| BC |
当
| AB |
| AC |
当
| AB |
| BC |
| 5 |
| 2 |
当
| AC |
| BC |
所以实数m的值为0或
| 5 |
| 2 |
点评：本题考查向量的数量积的运算，向量的垂直与平行关系的应用，考查计算能力．
练习册系列答案
相关题目
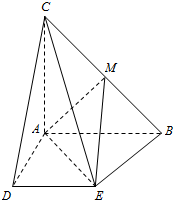在△ABC中，AB=AC，∠CAB=90°，且
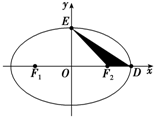如图F1、F2为椭圆C：