题目内容
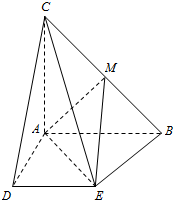 在△ABC中,AB=AC,∠CAB=90°,且
在△ABC中,AB=AC,∠CAB=90°,且| AD |
| AC |
| 1 |
| 2 |
(Ⅰ)求证:BC⊥AD;
(Ⅱ)当λ=
| 1 |
| 3 |
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间角
分析:(Ⅰ)由∠CAB=90°,知翻折后AD⊥AB,由C点在平面ADEB内的射影与点A重合,知CA⊥底面ABDE,由此能证明BC⊥AD.
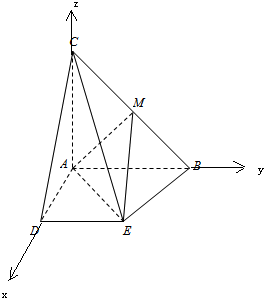
(Ⅱ)以A为原点,以AD为x轴,以AB为y轴,以AC为z轴,建立空间直角坐标系,利用向量法能求出直线BC与平面EAM所成角的正弦值.
(Ⅱ)以A为原点,以AD为x轴,以AB为y轴,以AC为z轴,建立空间直角坐标系,利用向量法能求出直线BC与平面EAM所成角的正弦值.
解答:
 (Ⅰ)证明:∵∠CAB=90°,∴CA⊥AB,
(Ⅰ)证明:∵∠CAB=90°,∴CA⊥AB,
∴翻折后AD⊥AB,
∵△DEC沿DE折起,C点在平面ADEB内的射影与点A重合,
∴CA⊥底面ABDE,
∵AD?底面ABCD,∴CA⊥AD,
∵AB∩CA=A,∴AD⊥平面ABC,
∵BC?平面ABC,∴BC⊥AD.
(Ⅱ)解:以A为原点,以AD为x轴,以AB为y轴,
以AC为z轴,建立空间直角坐标系,
设AB=AC=3,由题意知:
A(0,0,0),E(1,2,0),B(0,3,0),
C(0,0,
),M(0,
,
),
∴
=(0,
,
),
=(1,2,0),
=(0,-3,
),
设平面AME的法向量
=(x,y,z),
则
,
取z=
,得
=(2,-1,
),
设直线BC与平面EAM所成角为θ,
sinθ=|cos<
,
>|=|
|=
.
 (Ⅰ)证明:∵∠CAB=90°,∴CA⊥AB,
(Ⅰ)证明:∵∠CAB=90°,∴CA⊥AB,∴翻折后AD⊥AB,
∵△DEC沿DE折起,C点在平面ADEB内的射影与点A重合,
∴CA⊥底面ABDE,
∵AD?底面ABCD,∴CA⊥AD,
∵AB∩CA=A,∴AD⊥平面ABC,
∵BC?平面ABC,∴BC⊥AD.
(Ⅱ)解:以A为原点,以AD为x轴,以AB为y轴,
以AC为z轴,建立空间直角坐标系,
设AB=AC=3,由题意知:
A(0,0,0),E(1,2,0),B(0,3,0),
C(0,0,
| 3 |
| 3 |
| 2 |
| ||
| 2 |
∴
| AM |
| 3 |
| 2 |
| ||
| 2 |
| AE |
| BC |
| 3 |
设平面AME的法向量
| n |
则
|
取z=
| 3 |
| n |
| 3 |
设直线BC与平面EAM所成角为θ,
sinθ=|cos<
| BC |
| n |
| 3+3 | ||||
|
| ||
| 4 |
点评:本题考查异面直线的证明,考查直线与平面所成角的正弦值的求法,解题时要注意向量法的合理运用.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
如图是一组有规律的图案,第(1)个图案由4个基础图形组成,第(2)个图案由7个基础图形组成,…,第(670)个图案中的基础图形个数有( )


| A、2008 | B、2009 |
| C、2010 | D、2011 |
不等式x2-3x≤0的解集是( )
| A、{x|0<x≤3} |
| B、{x|0≤x<3} |
| C、{x|0≤x≤3} |
| D、{x|x≤0或x≥3} |
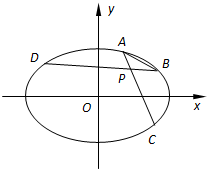 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E: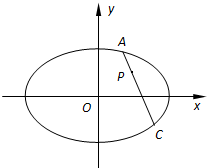 如图所示,在平面直角坐标系xOy中,过椭圆E:
如图所示,在平面直角坐标系xOy中,过椭圆E: