题目内容
在△ABC中,a、b边是方程x2-2
x+2=0的两个根,且2cos(A+B)=1.
(1)求角C的度数;
(2)求c边的长度.
| 3 |
(1)求角C的度数;
(2)求c边的长度.
考点:余弦定理,运用诱导公式化简求值
专题:解三角形
分析:(1)利用诱导公式求得cosC=-cos(A+B)进而根据已知条件求得cos(A+B)的值,求得cosC的值,则C可求得.
(2)利用韦达定理求得a+b和ab出值,进而利用余弦定理求得AB的值.
(2)利用韦达定理求得a+b和ab出值,进而利用余弦定理求得AB的值.
解答:
解:(1)cosC=cos(π-A-B)=-cos(A+B)=-
,
∴C=
.
(2)由题设:
∴AB2=AC2+BC2-2AC•BC•cosC=a2+b2-2abcos
=a2+b2+ab=(a+b)2-ab=12-2=10
∴AB=
.
| 1 |
| 2 |
∴C=
| 2π |
| 3 |
(2)由题设:
|
∴AB2=AC2+BC2-2AC•BC•cosC=a2+b2-2abcos
| 2π |
| 3 |
∴AB=
| 10 |
点评:本题主要考查了余弦定理的应用,二次方程的相关问题.考查了学生综合运用所学知识解决问题的能力.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
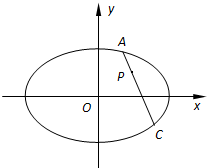 如图所示,在平面直角坐标系xOy中,过椭圆E:
如图所示,在平面直角坐标系xOy中,过椭圆E: