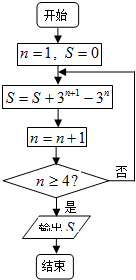
题目内容
设函数f(x)=ax2-(2a+1)x+2.
(Ⅰ)若f(x)>-x-1恒成立,求a的取值范围;
(Ⅱ)当a>0时,解不等式:f(x)>0.
(Ⅰ)若f(x)>-x-1恒成立,求a的取值范围;
(Ⅱ)当a>0时,解不等式:f(x)>0.
考点:二次函数的性质
专题:函数的性质及应用,不等式的解法及应用
分析:(I)若f(x)>-x-1恒成立,即ax2-2ax+3>0成立,等价于a=0或
,进而可得a的取值范围;
(Ⅱ)当a>0时,函数f(x)=ax2-(2a+1)x+2的图象是开口朝上与x轴交于(2,0)点和(
,0)点的抛物线,结合函数的图象,对a进行分类讨论可得不等式:f(x)>0的解集.
|
(Ⅱ)当a>0时,函数f(x)=ax2-(2a+1)x+2的图象是开口朝上与x轴交于(2,0)点和(
| 1 |
| a |
解答:
解:(I)若f(x)>-x-1恒成立,
则ax2-2ax+3>0恒成立,
即a=0或
,
解得:a∈[0,3),
故a的取值范围为[0,3);
(II)当a>0时,函数f(x)=ax2-(2a+1)x+2的图象是开口朝上与x轴交于(2,0)点和(
,0)点的抛物线,
若2<
,即0<a<
,f(x)>0的解集为:(-∞,2)∪(
,+∞);
若2=
,即a=
,f(x)>0的解集为:(-∞,2)∪(2,+∞);
若2>
,即a>
,f(x)>0的解集为:(-∞,
)∪(2,+∞);
则ax2-2ax+3>0恒成立,
即a=0或
|
解得:a∈[0,3),
故a的取值范围为[0,3);
(II)当a>0时,函数f(x)=ax2-(2a+1)x+2的图象是开口朝上与x轴交于(2,0)点和(
| 1 |
| a |
若2<
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
若2=
| 1 |
| a |
| 1 |
| 2 |
若2>
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
点评:本题考查的知识点是二次函数的图象和性质,恒成立问题,解二次不等式,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
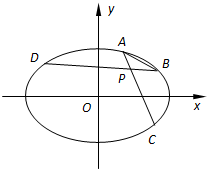 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E: