题目内容
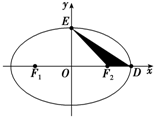 如图F1、F2为椭圆C:
如图F1、F2为椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| x0 |
| a |
| y0 |
| b |
(1)求椭圆C的标准方程;
(2)问是否存在过左焦点F1,的直线l,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意得e=
=
,S△DEF2=
(a-c)×b=1-
,由此能求出椭圆C的标准方程.
(2)当直线l的斜率不存在时,直线l的方程为x=-
,以PQ为直径的圆不过坐标原点;当直线l的斜率存在时,设直线l的方程为y=k(x+
),联立
,得(4k2+1)x2+8
k2x+12k2-4=0,由根与系数的关系,能求出直线方程为y=
x+
或y=-
x-
.
| c |
| a |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(2)当直线l的斜率不存在时,直线l的方程为x=-
| 3 |
| 3 |
|
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
解:(1)由题意得e=
=
,∴c=
a,b=
a,
S△DEF2=
(a-c)×b=
(a-
a)×
=
(1-
)a2=1-
,
∴a2=4,即a=2,∴b=1,c=
,
∴椭圆C的标准方程为
+y2=1.
(2)①当直线l的斜率不存在时,直线l的方程为x=-
联立
,解得
或
,
不妨令A(-
,
),B(-
,-
),
∴对应的“椭点”坐标P(-
,
),Q(-
,-
).而
•
=
≠0.
∴此时以PQ为直径的圆不过坐标原点.
②当直线l的斜率存在时,设直线l的方程为y=k(x+
),
联立
,消去y,得:(4k2+1)x2+8
k2x+12k2-4=0,
设A(x1,y1),B(x2,y2),则这两点的“椭点”坐标分别为P(
,y1),Q(
,y2),
由根与系数的关系,得x1+x2=
,x1x2=
,
若使得以PQ为直径的圆经这坐标原点,则OP⊥OQ,
而
=(
,y1),
=(
,y2),
∴
•
=0,
即
•
+y1•y2=0,
∴
=0,解得k=±
,
∴直线方程为y=
x+
或y=-
x-
.
| c |
| a |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
S△DEF2=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| a |
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
∴a2=4,即a=2,∴b=1,c=
| 3 |
∴椭圆C的标准方程为
| x2 |
| 4 |
(2)①当直线l的斜率不存在时,直线l的方程为x=-
| 3 |
联立
|
|
|
不妨令A(-
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
∴对应的“椭点”坐标P(-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| OP |
| OQ |
| 1 |
| 2 |
∴此时以PQ为直径的圆不过坐标原点.
②当直线l的斜率存在时,设直线l的方程为y=k(x+
| 3 |
联立
|
| 3 |
设A(x1,y1),B(x2,y2),则这两点的“椭点”坐标分别为P(
| x1 |
| 2 |
| x2 |
| 2 |
由根与系数的关系,得x1+x2=
-8
| ||
| 4k2+1 |
| 12k2-4 |
| 4k2+1 |
若使得以PQ为直径的圆经这坐标原点,则OP⊥OQ,
而
| OP |
| x1 |
| 2 |
| OQ |
| x2 |
| 2 |
∴
| OP |
| OQ |
即
| x1 |
| 2 |
| x2 |
| 2 |
∴
| 2k2-1 |
| 4k2+1 |
| ||
| 2 |
∴直线方程为y=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
不等式x2-3x≤0的解集是( )
| A、{x|0<x≤3} |
| B、{x|0≤x<3} |
| C、{x|0≤x≤3} |
| D、{x|x≤0或x≥3} |
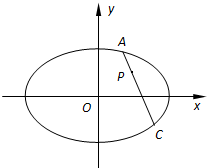 如图所示,在平面直角坐标系xOy中,过椭圆E:
如图所示,在平面直角坐标系xOy中,过椭圆E: