题目内容
设P是60°的二面角α-l-β内一点,PA⊥平面α,PB⊥平面β,A,B为垂足,PA=4,PB=2,则AB的长为 .
考点:与二面角有关的立体几何综合题
专题:空间角
分析:设平面PAB与二面角的棱l交于点Q,连结AQ、BQ得直线l⊥平面PAQB,由题意知∠AQB是二面角α-l-β的平面角,由此利用余弦定理能求出AB.
解答:
解:设平面PAB与二面角的棱l交于点Q,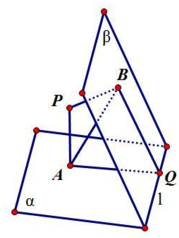
连结AQ、BQ得直线l⊥平面PAQB,
∵P是60°的二面角α-l-β内一点,PA⊥平面α,PB⊥平面β,
∴∠AQB是二面角α-l-β的平面角,∴∠AQB=60°,
∴△PAB中,∠APB=180°-60°=120°,PA=4,PB=2,
由余弦定理得:
AB2=PA2+PB2-2PA•PAcos120°
=42+22-2×4×2×(-
)=28,
∴AB=
=2
.
故答案为:2
.

连结AQ、BQ得直线l⊥平面PAQB,
∵P是60°的二面角α-l-β内一点,PA⊥平面α,PB⊥平面β,
∴∠AQB是二面角α-l-β的平面角,∴∠AQB=60°,
∴△PAB中,∠APB=180°-60°=120°,PA=4,PB=2,
由余弦定理得:
AB2=PA2+PB2-2PA•PAcos120°
=42+22-2×4×2×(-
| 1 |
| 2 |
∴AB=
| 28 |
| 7 |
故答案为:2
| 7 |
点评:本题考查直线与平面垂直的判定和二面角的概念,是中档题,解题时要注意利用正、余弦定理解三角形的灵活运用.

练习册系列答案
相关题目
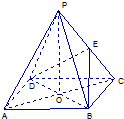 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.