题目内容
已知函数f（x）=x+
+17．
（Ⅰ）求函数f（x）的值域．
（Ⅱ）解不等式f（x）≤0．
| 16 |
| x |
（Ⅰ）求函数f（x）的值域．
（Ⅱ）解不等式f（x）≤0．
考点：其他不等式的解法,函数的值域,基本不等式
专题：不等式的解法及应用
分析：（Ⅰ）分x＞0和x＜0两种情况，分别利用基本不等式求得x+
的范围，可得函数f（x）的值域．
（Ⅱ）用穿根法求得不等式f（x）≤0的解集．
| 16 |
| x |
（Ⅱ）用穿根法求得不等式f（x）≤0的解集．
解答：
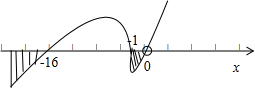解：（Ⅰ）函数f（x）的定义域是（-∞，0）∪（0，+∞），
当x＞0时，x+
≥2
=8，等号在x=
，即x=4成立．
因函数h(x)=x+
是奇函数，所以当x＜0时，x+
≤-8，
所以，函数f（x）的值域是（-∞，9]∪[25，+∞）．
（Ⅱ）∵f(x)=x+
+17，f（x）≤0，∴x+
+17≤0，
即
≤0，用穿根法求得不等式的解集为 x≤-16或-1≤x＜0，
所以，不等式f（x）≤0的解集是（-∞，-16]∪[-1，0）．
解：（Ⅰ）函数f（x）的定义域是（-∞，0）∪（0，+∞），当x＞0时，x+
| 16 |
| x |
x•
|
| 16 |
| x |
因函数h(x)=x+
| 16 |
| x |
| 16 |
| x |
所以，函数f（x）的值域是（-∞，9]∪[25，+∞）．
（Ⅱ）∵f(x)=x+
| 16 |
| x |
| 16 |
| x |
即
| (x+1)(x+16) |
| x |
所以，不等式f（x）≤0的解集是（-∞，-16]∪[-1，0）．
点评：本题主要考查利用基本不等式求函数的值域，用穿根法求分式不等式和高次不等式，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
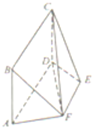如图，几何体ABCDEF中，四边形ABCD为矩形，且平面ABCD⊥平面ADEF，四边形ADEF为等腰梯形，AD∥EF，AD=2，AB=AF=1，∠DAF=60°．