题目内容
已知数列{an},其前n项和Sn=n2+n+1,则a3= .
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:利用“当n≥2时,an=Sn-Sn-1”即可得出an.(n≥2).
解答:
解:当n≥2时,an=Sn-Sn-1=n2+n+1-[(n-1)2+(n-1)+1]=2n.
∴a3=2×3=6.
故答案为:6.
∴a3=2×3=6.
故答案为:6.
点评:本题考查了通项公式与前n项和之间的关系,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
一个物体的运动方程为s=-t+t2,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
| A、8米/秒 | B、7米/秒 |
| C、6米/秒 | D、5米/秒 |
函数f(x)=
+
的定义域为( )
| 1 |
| x-1 |
| 2+x |
| A、[-2,+∞) |
| B、[-2,1)∪(1,+∞) |
| C、R |
| D、(-∞,-2] |

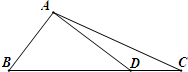 如图所示,在△ABC中,
如图所示,在△ABC中,