题目内容
设函数f(x)=2x+
-1(x<0),则f(x)有最 (填“大”或“小”)值为 .
| 1 |
| x |
考点:基本不等式
专题:不等式的解法及应用
分析:变形利用基本不等式即可得出.
解答:
解:∵x<0,
∴-x>0,
∴f(x)=-(-2x+
)-1≤-2
-1=-1-2
,当且仅当x=-
时取等号.
故f(x)有最大值为-1-2
.
故答案为:大,-1-2
.
∴-x>0,
∴f(x)=-(-2x+
| 1 |
| -x |
-2x•
|
| 2 |
| ||
| 2 |
故f(x)有最大值为-1-2
| 2 |
故答案为:大,-1-2
| 2 |
点评:本题考查了基本不等式的应用,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
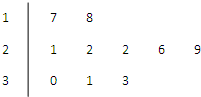 如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )
如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )| A、0.2 | B、0.4 |
| C、0.5 | D、0.6 |
