题目内容
函数f(x)=
+
的定义域为（ ）
| 1 |
| x-1 |
| 2+x |
| A、[-2，+∞） |
| B、[-2，1）∪（1，+∞） |
| C、R |
| D、（-∞，-2] |
考点：函数的值域
专题：函数的性质及应用
分析：根据题意，函数解析式的分母不为0，且二次根式的被开方数大于或等于0，解出即可．
解答：
解：∵函数f(x)=
+
，
∴应满足
，
解答x≥-2，且x≠1，
即定义域为[-2，1）∪（1，+∞）．
故选：B．
| 1 |
| x-1 |
| 2+x |
∴应满足
|
解答x≥-2，且x≠1，
即定义域为[-2，1）∪（1，+∞）．
故选：B．
点评：本题考查了求函数定义域的问题，求定义域即是求使函数解析式成立的自变量的取值范围，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
执行如图的程序，若输入的实数x=4，则输出结果为（ ）| A、4 | ||
| B、3 | ||
| C、2 | ||
D、
|
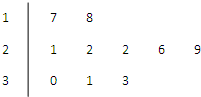如图是某公司10个销售店某月销售某产品数量（单位：台）的茎叶图，则数据落在区间[20，30）内的概率为（ ）| A、0.2 | B、0.4 |
| C、0.5 | D、0.6 |
在△ABC中，a=
b，A=2B，则cosB等于（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}是等差数列，a1=1，公差d≠0，若a1，a2，a5成等比数列，则a8=（ ）
| A、10 | B、15 | C、13 | D、14 |
如图，将1，2，3，4，5，6，7，8，9共9个数填入该图中，其中1，4，9已经如图填好．要求每一行的数字从左到右递增，每一列的数字从上到下递增，每一个数字只能填一次，则共有（ ）种不同的填法．| A、12 | B、24 | C、30 | D、10 |
若a＞0＞b，0＞c＞d则以下不等式中不成立的是（ ）
| A、a+c＞b+d | ||||
| B、a-d＞b-c | ||||
| C、ac＜bd | ||||
D、
|
已知函数f（x）=2x+a•2-x（x∈R），则对于任意实数a，函数f（x）不可能是（ ）
| A、奇函数 | B、偶函数 |
| C、单调递增函数 | D、单调递减函数 |