题目内容
已知cotα=2,tan(α-β)=-
,则tan(β-2α)= .
| 2 |
| 3 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:依题意,可求得tanα=
,tan(β-α)=
,利用两角差的正切tan(β-2α)=tan[(β-α)-α]=
即可求得答案.
| 1 |
| 2 |
| 2 |
| 3 |
| tan(β-α)-tanα |
| 1+tan(β-α)tanα |
解答:
解:∵cotα=2,tan(α-β)=-
,
∴tanα=
,tan(β-α)=
,
∴tan(β-2α)=tan[(β-α)-α]=
=
=
,
故答案为:
.
| 2 |
| 3 |
∴tanα=
| 1 |
| 2 |
| 2 |
| 3 |
∴tan(β-2α)=tan[(β-α)-α]=
| tan(β-α)-tanα |
| 1+tan(β-α)tanα |
| ||||
1+
|
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题考查两角和与差的正切函数,考查观察、运算与求解能力,属于中档题.

练习册系列答案
相关题目
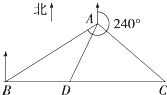 海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10
海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10