题目内容
已知等比数列{an}的各项均为正数,a1=2,anan+1=m•4n,n∈N*,
(1)求m的值及数列{an}的通项公式;
(2)是否存在等差数列{bn},使得a1b1+a2b2+…+anbn=(3n-4)•2n+1+8对任意n∈N*都成立?若存在,求出数列{bn}的通项公式;若不存在,请说明理由.
(1)求m的值及数列{an}的通项公式;
(2)是否存在等差数列{bn},使得a1b1+a2b2+…+anbn=(3n-4)•2n+1+8对任意n∈N*都成立?若存在,求出数列{bn}的通项公式;若不存在,请说明理由.
考点:等差数列与等比数列的综合
专题:综合题,等差数列与等比数列
分析:(1)先求出公比,即可求出数列{an}的通项公式,从而求出m的值;
(2)先猜想,再用数学归纳法进行证明.
(2)先猜想,再用数学归纳法进行证明.
解答:
解:(1)设an=2qn-1(q>0),则
=
=q2=4,
∴q=2,∴an=2n,
anan+1=m•4n=22n+1=2•4n,∴m=2.…(5分)
(2)存在等差数列bn=3n-1,使得a1b1+a2b2+…+anbn=(3n-4)•2n+1+8对任意n∈N*都成立.…(7分)
下面用数学归纳法证明:
(i)当n=1时,等式左边=a1b1=4,等式右边=(3-4)•22+8=4,所以等式成立.…(8分)
(ii)假设当n=k时等式成立,即a1b1+a2b2+…+akbk=(3k-4)•2k+1+8,…(9分)
则a1b1+a2b2+…+akbk+ak+1bk+1=(3k-4)•2k+1+8+(3k+2)•2k+1
=(3k-1)•2k+2+8=[3(k+1)-4]•2(k+1)+2+8…(11分)
这就是说,当n=k+1时,等式也成立.
综上(i)(ii)可知,等式对一切n∈N*都成立.故存在等差数列{bn},使得a1b1+a2b2+…+anbn=(3n-4)•2n+1+8对任意n∈N*都成立.…(12分)
| an+2 |
| an |
| an+1an+2 |
| anan+1 |
∴q=2,∴an=2n,
anan+1=m•4n=22n+1=2•4n,∴m=2.…(5分)
(2)存在等差数列bn=3n-1,使得a1b1+a2b2+…+anbn=(3n-4)•2n+1+8对任意n∈N*都成立.…(7分)
下面用数学归纳法证明:
(i)当n=1时,等式左边=a1b1=4,等式右边=(3-4)•22+8=4,所以等式成立.…(8分)
(ii)假设当n=k时等式成立,即a1b1+a2b2+…+akbk=(3k-4)•2k+1+8,…(9分)
则a1b1+a2b2+…+akbk+ak+1bk+1=(3k-4)•2k+1+8+(3k+2)•2k+1
=(3k-1)•2k+2+8=[3(k+1)-4]•2(k+1)+2+8…(11分)
这就是说,当n=k+1时,等式也成立.
综上(i)(ii)可知,等式对一切n∈N*都成立.故存在等差数列{bn},使得a1b1+a2b2+…+anbn=(3n-4)•2n+1+8对任意n∈N*都成立.…(12分)
点评:本题目主要考查了利用数列的递推公式求解数列的通项公式,考查数学归纳法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
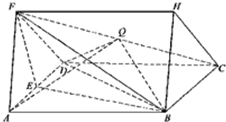 如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上.
如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上. 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=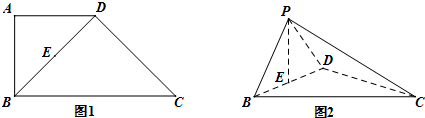
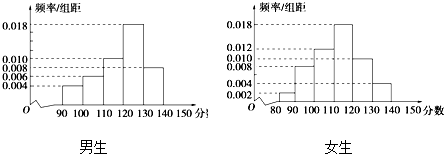
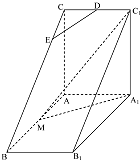 如图,直三棱柱ABC=A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点且
如图,直三棱柱ABC=A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点且