题目内容
二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1
(1)求f(x)表达式;
(2)若f(|x|)=m有四个不等根,则m的取值范围.
(1)求f(x)表达式;
(2)若f(|x|)=m有四个不等根,则m的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)运用待定系数法思想得出;设f(x)=ax2+bx+1,2a=2,a+b=0,求解即可.(2)画图象得出f(|x|)与y=m有4个交点,运用图象判断即可.
解答:
解:(1)f(0)=1
设f(x)=ax2+bx+1,
∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-ax2-bx-1=2x
2a=2,a+b=0
∴a=1,b=-1,
∴f(x)=x2-x,
(2)f(|x|)=x2-|x|,
f(
)=-
,
∵f(|x|)=m有四个不等根,
∴f(|x|)与y=m有4个交点,
∴据图得出:-
<m<0
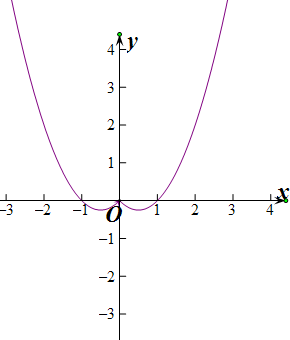
设f(x)=ax2+bx+1,
∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-ax2-bx-1=2x
2a=2,a+b=0
∴a=1,b=-1,
∴f(x)=x2-x,
(2)f(|x|)=x2-|x|,
f(
| 1 |
| 2 |
| 1 |
| 4 |
∵f(|x|)=m有四个不等根,
∴f(|x|)与y=m有4个交点,
∴据图得出:-
| 1 |
| 4 |
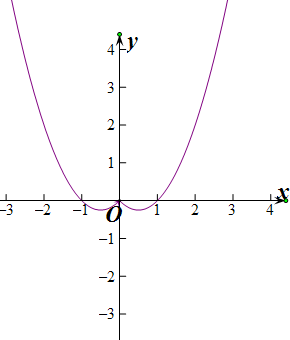
点评:本题考查了待定系数思想求解解析式,结合图象得出交点对应参变的范围,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设四个点P、A、B、C在同一球面上,且PA、PB、PC两两垂直,PA=3,PB=4,PC=5,那么这个球的表面积是( )
A、20
| ||
B、25
| ||
| C、25π | ||
| D、50π |
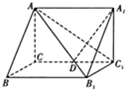 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,D是棱CC1的中点,A1D⊥AB1;
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,D是棱CC1的中点,A1D⊥AB1;