题目内容
设四个点P、A、B、C在同一球面上,且PA、PB、PC两两垂直,PA=3,PB=4,PC=5,那么这个球的表面积是( )
A、20
| ||
B、25
| ||
| C、25π | ||
| D、50π |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:设球的半径为R,由于四个点P、A、B、C在同一球面上,且PA、PB、PC两两垂直,可得球的直径为以PA、PB、PC邻边的长方体的对角线,利用(2R)2=32+42+52,解得即可.
解答:
解:设球的半径为R,
∵四个点P、A、B、C在同一球面上,且PA、PB、PC两两垂直,
∴球的直径为以PA、PB、PC邻边的长方体的对角线,
∴(2R)2=32+42+52,解得R2=
.
∴这个球的表面积是4πR2=50π.
故选:D.
∵四个点P、A、B、C在同一球面上,且PA、PB、PC两两垂直,
∴球的直径为以PA、PB、PC邻边的长方体的对角线,
∴(2R)2=32+42+52,解得R2=
| 50 |
| 4 |
∴这个球的表面积是4πR2=50π.
故选:D.
点评:本题考查了球的直径与长方体的对角线的关系、球的表面积计算公式,属于基础题.

练习册系列答案
相关题目
函数y=x2-4x+2,x∈[1,3]的最小值为( )
| A、0 | B、-1 | C、-2 | D、3 |
设集合A={(x,y)|
},则A=( )
|
A、
| |||||
| B、(3,-3) | |||||
| C、{(3,-3)} | |||||
| D、x=3,y=-3 |
在直角坐标系中,已知B(2,0),C(2,1),D(0,1),若P在△BCD内部和边界上运动,
=α
+β
(α,β都是实数),则2α-β的取值范围是( )
| OP |
| OB |
| OD |
| A、[-1,2] |
| B、[-1,3] |
| C、[-2,3] |
| D、[0,2] |
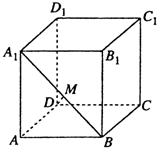 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.