题目内容
在△ABC中，a，b，c分别是角A，B，C的对边，且
=-
若b=
，a+c=4，则a的值为 ．
| cosB |
| cosC |
| b |
| 2a+c |
| 13 |
考点：正弦定理的应用
专题：计算题,解三角形
分析：运用正弦定理和两角和的正弦公式及诱导公式，求出角B，再由余弦定理，结合条件，解方程，即可得到a．
解答：
解：
=-
，
即有-2acosB=bcosC+ccosB，
即-2sinAcosB=sinBcosC+cosCsinB=sin（B+C）=sinA，
即有cosB=-
，
由于B为三角形的内角，则B=
，
又b2=a2+c2-2accosB，即有13=a2+c2+ac，
又a+c=4，
解得，a=1，c=3或a=3，c=1．
故答案为：1或3．
| cosB |
| cosC |
| b |
| 2a+c |
即有-2acosB=bcosC+ccosB，
即-2sinAcosB=sinBcosC+cosCsinB=sin（B+C）=sinA，
即有cosB=-
| 1 |
| 2 |
由于B为三角形的内角，则B=
| 2π |
| 3 |
又b2=a2+c2-2accosB，即有13=a2+c2+ac，
又a+c=4，
解得，a=1，c=3或a=3，c=1．
故答案为：1或3．
点评：本题考查正弦定理和余弦定理的运用，同时考查两角和的正弦公式和诱导公式及应用，考查运算能力，属于中档题．
练习册系列答案
相关题目
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则该几何体的体积为（ ）
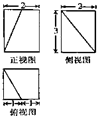
| A、9 | ||
| B、10 | ||
| C、11 | ||
D、
|
已知tanα=
，且点A（-4，a）在角α的终边上，则a的值是（ ）
| 3 |
A、4
| ||
B、-4
| ||
C、±4
| ||
D、
|
设集合A={（x，y）|
}，则A=（ ）
|
A、
| |||||
| B、（3，-3） | |||||
| C、{（3，-3）} | |||||
| D、x=3，y=-3 |
下列各组函数表示同一函数的是（ ）
A、f（x）=
| |||||
B、f（x）=
| |||||
| C、f（x）=1，g（x）=x0 | |||||
D、f（x）=x+1，g（x）=
|