题目内容
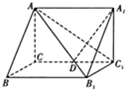 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,D是棱CC1的中点,A1D⊥AB1;
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,D是棱CC1的中点,A1D⊥AB1;(Ⅰ)求AA1的长;
(Ⅱ)求二面角A1-AB1=C1的余弦值.
考点:用空间向量求平面间的夹角,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(Ⅰ)建立坐标系运用A1D•AB1=0,运用坐标求解即可.
(Ⅱ)求解平面的法向量,运用A1D•AB1=0,得出
,再运用数量积求解cos<
,
>即可得出二面角的平面角的余弦值.
(Ⅱ)求解平面的法向量,运用A1D•AB1=0,得出
| n |
| n |
| A1D |
解答:
解:(Ⅰ)以C为原点建立如图所示的坐标系,设AA1=a,则A1=(0,A,
),D(0,
,0),
A(0,0,
),B1=(1,a,0),
=(1,a.-
),
=(0,-
,-
),
∵,A1D⊥AB1
∴A1D•AB1=0,
即-
+3=0,解得:a=
,
∴AA1的长为
.

(Ⅱ)设平面AA1B1的法向量为
=(x,y,z),
A1D•AB1=0,
∴
令z=1,y=0,x=
,
∴
=(
,0,1)
∵AD1⊥AB1,AD1⊥B1C1,
∴A1D⊥平面AB1C1,
平面AB1C1的法向量为
=(0,-
,-
),
cos<
,
>=
=-
,
二面角A1-AB1=C1的余弦值为
.
| 3 |
| a |
| 2 |
A(0,0,
| 3 |
| AB1 |
| 3 |
| A1D |
| a |
| 2 |
| 3 |
∵,A1D⊥AB1
∴A1D•AB1=0,
即-
| a2 |
| 2 |
| 6 |
∴AA1的长为
| 6 |

(Ⅱ)设平面AA1B1的法向量为
| n |
A1D•AB1=0,
∴
|
令z=1,y=0,x=
| 3 |
∴
| n |
| 3 |
∵AD1⊥AB1,AD1⊥B1C1,
∴A1D⊥平面AB1C1,
平面AB1C1的法向量为
| A1D |
| ||
| 2 |
| 3 |
cos<
| n |
| A1D |
-
| ||||
2•
|
| ||
| 6 |
二面角A1-AB1=C1的余弦值为
| ||
| 6 |
点评:本题考查了空间向量在求夹角,距离终点运用属于中档题,关键是求解法向量,数量积,计算准确.

练习册系列答案
相关题目
在等差数列{an}中,a1=2,a3+a5=10,则a7=( )
| A、5 | B、8 | C、10 | D、14 |
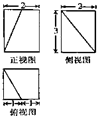
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )

| A、9 | ||
| B、10 | ||
| C、11 | ||
D、
|
在△ABC中,三边a,b,c与面积S的关系是S=
,则∠C=( )
| a2+b2-c2 |
| 4 |
| A、30° | B、60° |
| C、45° | D、90° |
 三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成的角等于
三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成的角等于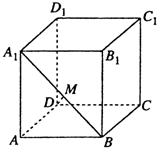 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.