题目内容
13.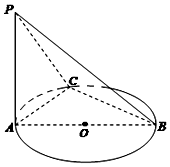 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 由题意可知,∠PCA为直线PC与底面ABC所成角,然后求解直角三角形得答案.
解答 解:如图,
∵PA垂直于⊙O所在平面,∴AC为PC在地面上的射影,
则∠PCA为斜线PC与底面所成角,
又AB为圆O的直径,∴AC⊥BC,在Rt△ACB中,
∵AB=2,BC=$\sqrt{3}$,∴AC=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}=1$,
在Rt△PAC中,∵PA=$\sqrt{3}$,AC=1,
∴tan∠PCA=$\frac{PA}{AC}=\sqrt{3}$,则∠PCA=60°.
∴直线PC与底面ABC所成角的大小为60°.
故选:C.
点评 本题考查直线与平面所成角,考查空间想象能力和思维能力,是基础题.

练习册系列答案
相关题目
3.不等式(3x+1)(1-2x)>0的解集是( )
| A. | $\{x|x<-\frac{1}{3}或x>\frac{1}{2}\}$ | B. | $\{x|-\frac{1}{3}<x<\frac{1}{2}\}$ | C. | $\{x|x>\frac{1}{2}\}$ | D. | $\{x|x>-\frac{1}{3}\}$ |
4.若f(x)为奇函数,且x0是函数y=f(x)-ex的一个零点,在下列函数中,-x0一定是其零点的函数是( )
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•e-x+1 | C. | y=f(x)•e-x-1 | D. | y=f(x)•ex+1 |
18.将函数$y=4sin({4x+\frac{π}{6}})$的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移$\frac{π}{6}$个单位,则所得函数图象的一个对称中心为( )
| A. | (0,0) | B. | $({\frac{π}{3},0})$ | C. | $({\frac{π}{12},0})$ | D. | $({\frac{5}{8}π,0})$ |
2.若不等式n2-n(λ+1)+7≥λ,对一切n∈N*恒成立,则实数λ的取值范围( )
| A. | λ≤3 | B. | λ≤4 | C. | 2≤λ≤3 | D. | 3≤λ≤4 |
10.棱长为1的正方体截去一部分之后余下的几何体,其三视图如图所示,则余下几何体体积的最小值为( )
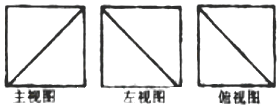

| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |