题目内容
在三角形ABC中，AB=AC，点P为线段AB上一点，且
=λ
．
（Ⅰ）若
=
+
，求λ的值；
（Ⅱ）若∠A=120°，且
•
＞4
•
，求实数λ的取值范围．
| AP |
| AB |
（Ⅰ）若
| CP |
| 3 |
| 4 |
| CA |
| 1 |
| 4 |
| CB |
（Ⅱ）若∠A=120°，且
| CP |
| AB |
| AP |
| PB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：对第（Ⅰ）问，根据平面向量基本定理及已知条件
=λ
，将向量
用向量
，
线性表示，再与向量
+
对比即可得λ的值；
对第（Ⅱ）问，由∠A=120°，可将
，
作为一组基底，从而
，
，
都用基底表示，于是得到一个关于λ的不等式，结合此不等式的解和0≤λ≤1可知λ的范围．
| AP |
| AB |
| CP |
| CA |
| CB |
| 3 |
| 4 |
| CA |
| 1 |
| 4 |
| CB |
对第（Ⅱ）问，由∠A=120°，可将
| AB |
| AC |
| CP |
| AP |
| PB |
解答：
解：（Ⅰ）
=
+
=
+λ
=
+λ(
-
)=(1-λ)
+λ
，
即
=(1-λ)
+λ
，
由题设知
=
+
，根据平面向量基本定理，有
，
∴λ=
．
（Ⅱ）设等腰三角形的腰长为a，则
•
=(
+
)•
=
•
+
•
=|
||
|cos(180°-120°)+|
||
|=
a2+λa2，
•
=
•(
-
)=
•
-
2=λa2-λ2a2．
由
•
＞4
•
，得
a2+λa2＞4λa2-4λ2a2，
即8λ2-6λ+1＞0，解得λ＞
，或λ＜
．
又点P在线段AB上，所以0≤λ≤1，
故λ的取值范围是[0，
)∪(
，1]．
| CP |
| CA |
| AP |
| CA |
| AB |
| CA |
| CB |
| CA |
| CA |
| CB |
即
| CP |
| CA |
| CB |
由题设知
| CP |
| 3 |
| 4 |
| CA |
| 1 |
| 4 |
| CB |
|
∴λ=
| 1 |
| 4 |
（Ⅱ）设等腰三角形的腰长为a，则
| CP |
| AB |
| CA |
| AP |
| AB |
| CA |
| AB |
| AP |
| AB |
=|
| CA |
| AB |
| AP |
| AB |
| 1 |
| 2 |
| AP |
| PB |
| AP |
| AB |
| AP |
| AP |
| AB |
| AP |
由
| CP |
| AB |
| AP |
| PB |
| 1 |
| 2 |
即8λ2-6λ+1＞0，解得λ＞
| 1 |
| 2 |
| 1 |
| 4 |
又点P在线段AB上，所以0≤λ≤1，
故λ的取值范围是[0，
| 1 |
| 4 |
| 1 |
| 2 |
点评：本题考查了平面向量的数量积运算，向量的加、减法运算，数乘运算，向量共线的充要条件及平面向量基本定理，涉及的知识点较多，关键是通过计算与变形，使所有向量均用一组基向量表示，从而建立了关于λ的不等式，最终达到了求解的目的．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
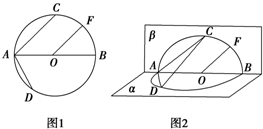如图1，⊙O的直径AB=4，点C、D为⊙O上两点，且∠CAB=45°，F为
在平面直角坐标系xOy中，已知AB是椭圆
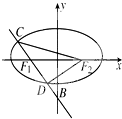已知椭圆