题目内容
在平面直角坐标系xOy中,已知双曲线
-
=1(a>0)的一条渐近线方程为3x+2y=0,点A为双曲线C的右顶点,圆O的方程为x2+y2=1.
(1)求a的值;
(2)点M为平面内一动点,过M引圆O的切线MN(N为切点),若
=
,求动点M的轨迹方程.
| x2 |
| a2 |
| y2 |
| 9 |
(1)求a的值;
(2)点M为平面内一动点,过M引圆O的切线MN(N为切点),若
| MN |
| MA |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由双曲线
-
=1(a>0)的渐近线方程为3x±ay=0,结合已知条件求出a=2.
(2)由(1)知A(2,0),设M(x,y),N(cosθ,sinθ),0≤θ<π,则(x-cosθ)2+(y-sinθ)2+1=x2+y2,由此根据已知条件得到
=
,从而得到
=
,由此能求出动点M的轨迹方程.
| x2 |
| a2 |
| y2 |
| 9 |
(2)由(1)知A(2,0),设M(x,y),N(cosθ,sinθ),0≤θ<π,则(x-cosθ)2+(y-sinθ)2+1=x2+y2,由此根据已知条件得到
| ||
|
| 2 |
| ||
|
| 2 |
解答:
解:(1)∵双曲线
-
=1(a>0)的渐近线方程为3x±ay=0,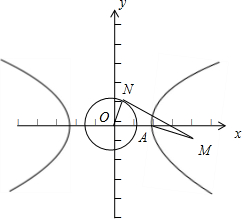
由其中一条渐近线方程为3x+2y=0,
解得a=2.
(2)由(1)知双曲线方程为
-
=1,
∵点A为双曲线C的右顶点,∴A(2,0),
设M(x,y),∵圆O的方程为x2+y2=1,
∴N(cosθ,sinθ),0≤θ<π,
则(x-cosθ)2+(y-sinθ)2+1=x2+y2,
解得(x-cosθ)2+(y-sinθ)2=x2+y2-1,
∵
=
,∴
=
,
∴
=
,
整理,得:x2+y2-8x+9=0.
∴动点M的轨迹方程为x2+y2-8x+9=0.
| x2 |
| a2 |
| y2 |
| 9 |

由其中一条渐近线方程为3x+2y=0,
解得a=2.
(2)由(1)知双曲线方程为
| x2 |
| 4 |
| y2 |
| 9 |
∵点A为双曲线C的右顶点,∴A(2,0),
设M(x,y),∵圆O的方程为x2+y2=1,
∴N(cosθ,sinθ),0≤θ<π,
则(x-cosθ)2+(y-sinθ)2+1=x2+y2,
解得(x-cosθ)2+(y-sinθ)2=x2+y2-1,
∵
| MN |
| MA |
| 2 |
| ||
|
| 2 |
∴
| ||
|
| 2 |
整理,得:x2+y2-8x+9=0.
∴动点M的轨迹方程为x2+y2-8x+9=0.
点评:本题考查抛物线中参数的求法,考查动点M的轨迹方程的求法,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为 在极坐标系中,已知三点O(0,0),A(2,
在极坐标系中,已知三点O(0,0),A(2,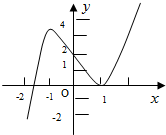 如图,是定义域为R的函数f(x)的图象,f′(x)是函数f(x)的导函数,则不等式xf′(x)>0的解集为
如图,是定义域为R的函数f(x)的图象,f′(x)是函数f(x)的导函数,则不等式xf′(x)>0的解集为