题目内容
已知函数f(x)=ax3+|x-a|,a∈R.
(1)若a=-1,求函数y=f(x)(x∈[0,+∞)的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
(1)若a=-1,求函数y=f(x)(x∈[0,+∞)的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
考点:利用导数研究曲线上某点切线方程,根的存在性及根的个数判断,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)利用导数的几何意义,求出切线的斜率,即可求出图象在x=1处的切线方程;
(2)若g(x)=x4,方程等价于x=a或
或
,分类讨论,即可讨论方程f(x)=g(x)的实数解的个数;
(3)确定函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0,对任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)=1024,所以[
,
]⊆[f(a+2),+∞),即可得出结论.
(2)若g(x)=x4,方程等价于x=a或
|
|
(3)确定函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0,对任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)=1024,所以[
| 1024 |
| f(a+2) |
| 1024 |
| f(a) |
解答:
解:(1)当a=-1,x∈[0,+∞)时,f(x)=-x3+x+1,从而f′(x)=-3x2+1.
当x=1时,f(1)=1,f′(1)=-2,
所以函数y=f(x) (x∈[0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
即2x+y-3=0. …(3分)
(2)f(x)=g(x)即为ax3+|x-a|=x4.
所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.
此方程等价于x=a或
或
…(6分)
所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;
当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;
当a≤-1时,方程f(x)=g(x)有两个不同的解a,1. …(9分)
(3)当a>0,x∈(a,+∞)时,f(x)=ax3+x-a,f′(x)=3ax2+1>0,
所以函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0.
所以当x∈[a,a+2]时,f(x)∈[f(a),f(a+2)],
∈[
,
],
当x∈[a+2,+∞)时,f(x)∈[f(a+2),+∞). …(11分)
因为对任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)=1024,
所以[
,
]⊆[f(a+2),+∞). …(13分)
从而
≥f(a+2).
所以f 2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.
因为a>0,显然a=1满足,而a≥2时,均不满足.
所以满足条件的正整数a的取值的集合为{1}. …(16分)
当x=1时,f(1)=1,f′(1)=-2,
所以函数y=f(x) (x∈[0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
即2x+y-3=0. …(3分)
(2)f(x)=g(x)即为ax3+|x-a|=x4.
所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.
此方程等价于x=a或
|
|
所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;
当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;
当a≤-1时,方程f(x)=g(x)有两个不同的解a,1. …(9分)
(3)当a>0,x∈(a,+∞)时,f(x)=ax3+x-a,f′(x)=3ax2+1>0,
所以函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0.
所以当x∈[a,a+2]时,f(x)∈[f(a),f(a+2)],
| 1024 |
| f(x) |
| 1024 |
| f(a+2) |
| 1024 |
| f(a) |
当x∈[a+2,+∞)时,f(x)∈[f(a+2),+∞). …(11分)
因为对任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)=1024,
所以[
| 1024 |
| f(a+2) |
| 1024 |
| f(a) |
从而
| 1024 |
| f(a+2) |
所以f 2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.
因为a>0,显然a=1满足,而a≥2时,均不满足.
所以满足条件的正整数a的取值的集合为{1}. …(16分)
点评:本题考查利用导数研究曲线上某点切线方程,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
从10张分别标有数字1,2,3,4,5,6,7,8,9,10的卡片中抽取4张卡片,则这4卡片上数字从小到大成等差数列的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
a>b>1,P=
,Q=
(lga+lgb),R=
,则( )
| lga•lgb |
| 1 |
| 2 |
| a+b |
| 2 |
| A、.R<P<Q |
| B、.P<Q<R |
| C、Q<P<R |
| D、.P<R<Q |
已知椭圆
+
=1的左、右焦点分别为F1,F2,P为椭圆上一点,当|PF1|=λ|PF2|时λ的取值范围( )
| x2 |
| 9 |
| y2 |
| 8 |
| A、[1,3] | ||
| B、[1,2] | ||
C、[
| ||
D、[
|
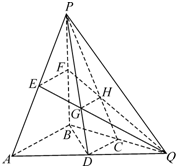 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
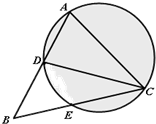 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.