题目内容
已知函数f(x)=ln(1+x)-
,若x≥0时,f(x)≤0,则λ的最小值为( )
| x(1+λx) |
| 1+x |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
考点:导数在最大值、最小值问题中的应用
专题:计算题,导数的概念及应用
分析:由于已知函数的最大值是0,故可先求出函数的导数,研究其单调性,确定出函数的最大值,利用最大值小于等于0求出参数λ的取值范围,即可求得其最小值.
解答:
解:(I)由已知,f(0)=0,f′(x)=
,且f′(0)=0,
若λ<
,则当0<x<2(1-2λ)时,f′(x)>0,所以当0<x<2(1-2λ)时,f(x)>0,
若λ≥
,则当x≥0时,f′(x)≤0,所以当x≥0时,f(x)≤0,
综上,λ的最小值为
.
故选:B.
| (1-2λ)x-λx2 |
| (1+x)2 |
若λ<
| 1 |
| 2 |
若λ≥
| 1 |
| 2 |
综上,λ的最小值为
| 1 |
| 2 |
故选:B.
点评:本题考查导数知识的运用,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集U=R,函数y=lg(2-x)的定义域为A,集合B={x|1<x<3},则(∁UA)∩B等于( )
| A、[2,3) |
| B、(1,2) |
| C、(2,3) |
| D、[1,2) |
从10张分别标有数字1,2,3,4,5,6,7,8,9,10的卡片中抽取4张卡片,则这4卡片上数字从小到大成等差数列的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
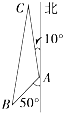 我舰在敌岛A处南偏西50°的B处,且AB距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,则速度大小为( )
我舰在敌岛A处南偏西50°的B处,且AB距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,则速度大小为( )| A、28海里/小时 | ||
| B、14海里/小时 | ||
C、14
| ||
| D、20海里/小时 |
正数x,y,z满足:5z-3x≤y≤4z-x,z•lny≥x+z•lnz,则
的最大值为( )
| y |
| x |
| A、7 | B、8 | C、9 | D、10 |
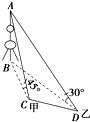 要测量底部不能到达的东方明珠电视塔的高度,在黄浦江西岸选择甲、乙两观测点,在甲、乙两点测得塔顶的仰角分别为45°、30°,在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°,甲、乙两地相距500米,则电视塔在这次测量中的高度是( )
要测量底部不能到达的东方明珠电视塔的高度,在黄浦江西岸选择甲、乙两观测点,在甲、乙两点测得塔顶的仰角分别为45°、30°,在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°,甲、乙两地相距500米,则电视塔在这次测量中的高度是( )A、100
| ||
| B、400米 | ||
C、200
| ||
| D、500米 |
a>b>1,P=
,Q=
(lga+lgb),R=
,则( )
| lga•lgb |
| 1 |
| 2 |
| a+b |
| 2 |
| A、.R<P<Q |
| B、.P<Q<R |
| C、Q<P<R |
| D、.P<R<Q |
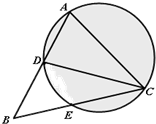 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.