题目内容
f(x)是偶函数,定义域是(-∞,+∞),在[0,+∞)上f(x)是减函数,那么f(-
)与f(a2-a+1)(a∈R)的大小关系是( )
| 3 |
| 4 |
A、f(-
| ||
B、f(-
| ||
C、f(-
| ||
D、f(-
|
考点:函数的定义域及其求法
专题:函数的性质及应用,不等式的解法及应用
分析:由函数的奇偶性和单调性得到f(-
)=f(
)≥f(a2-a++1),则答案可求.
| 3 |
| 4 |
| 3 |
| 4 |
解答:
解:∵f(x)是偶函数,定义域是(-∞,+∞),在[0,+∞)上f(x)是减函数,
∴a2-a+1=(a-
)2+
≥
,
∴f(-
)=f(
)≥f(a2-a++1).
故选:B.
∴a2-a+1=(a-
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴f(-
| 3 |
| 4 |
| 3 |
| 4 |
故选:B.
点评:本题考查了函数奇偶性和单调性的性质,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知椭圆
+
=1的左、右焦点分别为F1,F2,P为椭圆上一点,当|PF1|=λ|PF2|时λ的取值范围( )
| x2 |
| 9 |
| y2 |
| 8 |
| A、[1,3] | ||
| B、[1,2] | ||
C、[
| ||
D、[
|
已知空间四边形ABCD中,棱AB,AC,AD两两互相垂直AB=AC=2,AD=
,则成60°的二面角是( )
| 6 |
| A、B-AD-C |
| B、D-BC-A |
| C、C-BD-A |
| D、B-CD-A |
设变量x,y满足约束条件
.若目标函数z=ax+y在点(1,2)处取得最大值,则a的取值范围为( )
|
| A、(1,+∞) |
| B、(-∞,-1) |
| C、(-1,1) |
| D、[-1,1] |
已知集合M={x|sinx>cosx,0<x<π}和N={x|sin2x>cos2x,0<x<π},则M与N的交集为( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
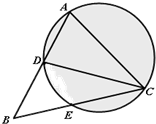 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.