题目内容
已知直线a2x-b2y=1，其中a、b∈R，且ab≠0，则倾斜角a的取值范围为 ．
考点：直线的倾斜角
专题：直线与圆
分析：由已知中直线a2x-b2y=1，其中a、b∈R，且ab≠0，先求出直线斜率的范围，进而可得倾斜角a的取值范围．
解答：
解：∵直线a2x-b2y=1中a、b∈R，且ab≠0，
故直线的斜率k=(
)2＞0，
故倾斜角a的取值范围为（0，
），
故答案为：（0，
）
故直线的斜率k=(
| a |
| b |
故倾斜角a的取值范围为（0，
| π |
| 2 |
故答案为：（0，
| π |
| 2 |
点评：本题考查的知识点是直线的倾斜角，熟练掌握直线倾斜角与斜率的关系，是解答的关键．
练习册系列答案
走进文言文系列答案
相关题目
在塔底的水平面上某点测得塔顶的仰角为θ，由此点向塔底沿直线行走30米，测得塔顶的仰角为2θ，再向塔前进若x=-
是f（x）=cosx+asinx的对称轴，则f（x）=cosx+asinx的初相是（ ）
| π |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
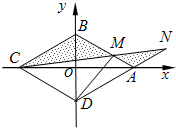如图，菱形ABCD的边长为2，∠BAD=60°，M为AB边上不与端点重合的动点，且CM与DA分别延长后交于点N，若以菱形的对角线所在直线为坐标轴建立平面直角坐标系，并设BM=2t （0＜t＜1）．