��Ŀ����
9����֪����A��ͬʱ���������������ʵĺ���f��x����ȫ�壮�ٺ���f��x�����䶨�������ǵ���������
��f��x���Ķ������ڴ�������[a��b]��ʹ��f��x����[a��b]�ϵ�ֵ��Ϊ[$\frac{a}{2}��\frac{b}{2}$]��
��1���ж�f��x��=x3�Ƿ�����M�����ǣ������������ڵ�����[a��b]�������ǣ�˵�����ɣ�
��2�����Ƿ����ʵ��t��ʹ��h��x��=$\sqrt{x-1}+t��M$�������ڣ���ʵ��t��ȡֵ��Χ���������ڣ�˵�����ɣ�
���� ��1�����Կ���g��x��Ϊ�����������������٣�������x3=$\frac{x}{2}$��������ͬ�Ľ⣬�Ӷ����������ڣ��Ӷ�˵��g��x������M���ҿ�д����������ڵ�����[a��b]��
��2�����õ����ɵú���h��x���ڶ�����[1��+�ޣ���������������h��x����M�������a��b��[1��+�ޣ�����a��b��ʹ��h��a��=$\frac{a}{2}$��h��b��=$\frac{b}{2}$����a-2$\sqrt{a-1}$-2t=0����b-2$\sqrt{b-1}$-2t=0����$\sqrt{x-1}$=y��x��1������y��0�����ǹ���y�ķ���y2-2y+1-2t=0��[0��+�ޣ�����2������ʵ�������ö��κ������������t�ķ�Χ��
��� �⣺��1��g��x��=x3��R��Ϊ���������������ʢ٣�
��x3=$\frac{x}{2}$�ã�x=0����x=��$\frac{\sqrt{2}}{2}$��
���������ʢڣ�
��g��x������M��������ڵ�����[a��b]Ϊ[-$\frac{\sqrt{2}}{2}$��0]��[0��$\frac{\sqrt{2}}{2}$]����[-$\frac{\sqrt{2}}{2}$��$\frac{\sqrt{2}}{2}$]��
��2������h��x���Ķ�������[1��+�ޣ���
��x��1ʱ��h�䣨x��=$\frac{1}{2\sqrt{x-1}}$��0���ʺ���h��x����[1��+�ޣ�������������
��h��x����M�������a��b��[1��+�ޣ�����a��b��
ʹ��h��a��=$\frac{a}{2}$��h��b��=$\frac{b}{2}$����a-2$\sqrt{a-1}$-2t=0����b-2$\sqrt{b-1}$-2t=0��
��$\sqrt{x-1}$=y��x��1������y��0��
���ǹ���y�ķ���y2-2y+1-2t=0��[0��+�ޣ������������ȵ�ʵ����
��u��y��=y2-2y+1-2t��
��$\left\{\begin{array}{l}{����0}\\{u��0����0}\end{array}\right.$����t�ʣ�0��$\frac{1}{2}$]��
���� ���麯�������ԵĶ��壬����ֵ��Ķ��壬f��x���������ʢڱ�˵������f��x��=$\frac{x}{2}$������������ͬ�⣬�Լ�һԪ���η���ʵ�����ĸ������б�ʽ���Ĺ�ϵ��

| A�� | [-1��3] | B�� | [4��8] | C�� | [1��3] | D�� | [2��3] |
| A�� | a��b��c | B�� | a��c��b | C�� | b��c��a | D�� | b��a��c |
| A�� | ��1��3�� | B�� | ��1��3] | C�� | [1��3�� | D�� | [1��3] |
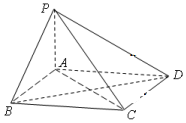 ��ͼ������P-ABCD�У�����ABCDΪ���Σ�PA��ƽ��ABCD
��ͼ������P-ABCD�У�����ABCDΪ���Σ�PA��ƽ��ABCD