Question

离心率为

1

2

的椭圆C₁与双曲线C₂有相同的焦点，且椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离依次构成等差数列，则双曲线C₂的离心率等于（　　）

• A、

  15

  3

• B、

  15

  5

• C、

  21

  3

• D、

  21

  7

Answer 1

考点：双曲线的简单性质,椭圆的简单性质

专题：综合题,圆锥曲线的定义、性质与方程

分析：求出椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离，利用等差数列的性质，即可得出结论．

解答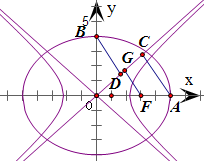： 解：设椭圆方程为

x2

a2

+

y2

b2

=1（a＞b＞0），双曲线方程为

x2

m2

-

y2

n2

=1（m＞0，n＞0）
它们一个公共的焦点为F（c，0）
∵椭圆长轴端点A到双曲线的渐近线nx-my=0的距离|AC|=

an

n2+m2

=

an

c

=2n，
椭圆短轴端点B到双曲线的渐近线nx-my=0的距离|BD|=

bm

c

椭圆焦点F到双曲线的渐近线nx-my=0的距离|FG|=

cn

c

=n，
∴2•

bm

c

=2n+n，
∵

c

a

=

1

2

，
∴a=2c，
∴b=

a2-c2

=

3

c，
∴2

3

m=3n，
∴m=

3

2

n，
∴c=

m2+n2

=

7

2

n，
∴e=

c

m

=

7 2 n

3 2 n

=

21

3

．
故选：C．

点评：本题给出共焦点的椭圆与双曲线，在已知点到直线的距离成等差数列情况下，求离心率的分式的值，着重考查了椭圆、双曲线的标准方程和简单几何性质等知识，属于中档题．