题目内容
在△ABC中,角A<B是sinA<sinB的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先看由角A<B能否得到sinA<sinB:讨论A,B∈(0,
]和A∈(0,
),B∈(
,π)两种情况,并结合y=sinx在(0,
]单调性及0<A+B<π即可得到sinA<sinB;然后看由sinA<sinB能否得到A<B:根据上一步的讨论方法以及y=sinx的单调性即可得到sinA<sinB,所以得到角A<B是sinA<sinB的充要条件.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:
解:(1)△ABC中,角A<B:
若0<A<B≤
,根据y=sinx在(0,
]上单调递增得到sinA<sinB;
若0<A<
,
<B<π,∵0<A+B<π,∴0<A<π-B<
,所以sinA<sin(π-B)=sinB;
∴角A<B能得到sinA<sinB;
即A<B能得到sinA<sinB;
∴角A<B是sinA<sinB的充分条件;
(2)若sinA<sinB:
A,B∈(0,
]时,y=sinx在(0,
]上单调递增,所以由sinA<sinB,得到A<B;
A∈(0,
),B∈(
,π)时,显然满足A<B;
即sinA<sinB能得到A<B;
∴A<B是sinA<sinB的必要条件;
综合(1)(2)得角A<B,是sinA<sinB的充要条件.
故选C.
若0<A<B≤
| π |
| 2 |
| π |
| 2 |
若0<A<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴角A<B能得到sinA<sinB;
即A<B能得到sinA<sinB;
∴角A<B是sinA<sinB的充分条件;
(2)若sinA<sinB:
A,B∈(0,
| π |
| 2 |
| π |
| 2 |
A∈(0,
| π |
| 2 |
| π |
| 2 |
即sinA<sinB能得到A<B;
∴A<B是sinA<sinB的必要条件;
综合(1)(2)得角A<B,是sinA<sinB的充要条件.
故选C.
点评:考查充分条件、必要条件、充要条件的概念,以及正弦函数y=sinx在(0,
]上的单调性,通过y=sinx在(0,π)的图象看函数的取值情况,及条件0<A+B<π.
| π |
| 2 |

练习册系列答案
相关题目
已知△ABC的三个顶点A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC的内部及边界运动,则z=x-y( )
| A、在点A处有最大值-2 |
| B、在点B处有最大值-3 |
| C、在点A处有最小值-2 |
| D、在点C处有最大值1 |
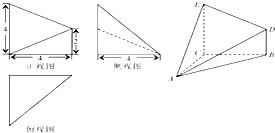 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )| A、32 | ||
| B、16 | ||
C、
| ||
| D、40 |
圆x2+y2=1与圆(x-3)2+(y+4)2=25的位置关系是( )
| A、相离 | B、相交 | C、内切 | D、外切 |