题目内容
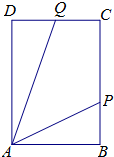 如图,ABCD是长方形海域,其中AB=10海里,AD=10
如图,ABCD是长方形海域,其中AB=10海里,AD=10| 2 |
| π |
| 4 |
(1)试建立S与tanθ的关系式,并指出tanθ的取值范围;
(2)求S的最大值,并指出此时θ的值.
考点:解三角形的实际应用
专题:解三角形
分析:(1)先分别求得△APB和△ADQ的面积,进而根据作差表示出S并根据图象求得tanθ的取值范围.
(2)利用基本不等式求得S的最小值,并求得取得等号时tanθ的值.
(2)利用基本不等式求得S的最小值,并求得取得等号时tanθ的值.
解答:
解:(1)在Rt△APB中,BP=10tanθ,S△ABP=
×10×10tanθ=50tanθ
在Rt△ADQ中,DQ=10
tan(
-θ),S△ADQ=
×10
×10
tan(
-θ)=100tan(
-θ)
∴S=100
-50tanθ-100tan(
-θ)=100
-50tanθ-100×
,
其中
,解得:3-2
≤tanθ≤1
∴S=100
-50tanθ-100×
,3-2
≤tanθ≤1.
(2)∵tanθ>0,S=100
-50(tanθ+2×
)=100
-50(tanθ+1+
-3)≤100
-50(2
-3)=100
-50,
当且仅当tanθ+1=
时取等号,亦即tanθ=1时,Smax=100
-50
∵θ∈(0,
),
∴θ=
答:当θ=
时,S有最大值100
-50.
| 1 |
| 2 |
在Rt△ADQ中,DQ=10
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
∴S=100
| 2 |
| π |
| 4 |
| 2 |
| 1-tanθ |
| 1+tanθ |
其中
|
| 2 |
∴S=100
| 2 |
| 1-tanθ |
| 1+tanθ |
| 2 |
(2)∵tanθ>0,S=100
| 2 |
| 1-tanθ |
| 1+tanθ |
| 2 |
| 4 |
| tanθ+1 |
| 2 |
(tanθ+1)•
|
| 2 |
当且仅当tanθ+1=
| 4 |
| tanθ+1 |
| 2 |
∵θ∈(0,
| π |
| 2 |
∴θ=
| π |
| 4 |
答:当θ=
| π |
| 4 |
| 2 |
点评:本题主要考查了解三角形实际应用的问题,利用基本不等式求最值.注重对学生综合素质的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
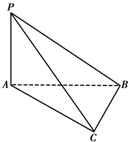 如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )
如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )| A、一对 | B、两对 | C、三对 | D、四对 |