题目内容
将编号为1，2，3，4，5，6的六个小球排成一列，要求1号球与2号球必须相邻，4号球、5号球、6号球互不相邻，则不同的排法种数有（ ）
| A、4 | B、24 | C、72 | D、144 |
考点：计数原理的应用
专题：排列组合
分析：根据题意，第一步用捆绑法，先将1号球与2号球，看作一个元素，考虑两者的顺序，再其与3号球进行全排列，可以满足1号球与2号球必须相邻，排好后，有3个空位，第二步用插空法，在3个空位中任取3个，安排4号球、5号球、6号球；由排列数公式可得每一步的情况数目，由分步计数原理计算可得答案．
解答：
解：根据题意，先将1号球与2号球，看作一个元素，考虑两者的顺序，有A22=2种情况，
再将1号球与2号球这个大元素与3号球全排列列，有A22=2种情况，排好后，有3个空位，
最后在3个空位中插入4号球、5号球、6号球，有A33=6种情况，
由分步计数原理可得，共有2×2×6=24种情况；
故选B．
再将1号球与2号球这个大元素与3号球全排列列，有A22=2种情况，排好后，有3个空位，
最后在3个空位中插入4号球、5号球、6号球，有A33=6种情况，
由分步计数原理可得，共有2×2×6=24种情况；
故选B．
点评：本题考查排列、组合的运用，关键要掌握特殊问题的处理方法，如相邻问题用捆绑法，不相邻问题用插空法．
练习册系列答案
相关题目
若已知△ABC的周长为9，且a：b：c=3：2：4，则cosC的值为（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知点F1，F2分别是椭圆
+
=1（a＞b＞0）的左、右焦点，点P是椭圆上的一个动点，若使得满足△PF1F2是直角三角形的动点P恰好有6个，则该椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知p：|x-2|＜3，q：0＜x＜5，那么p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
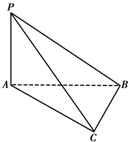如图所示，已知PA垂直于△ABC所在平面，且∠ACB=90°，连结PB、PC，则图形中互相垂直的平面有（ ）| A、一对 | B、两对 | C、三对 | D、四对 |
在程序框图中处理框的功能表示（ ）
| A、输入信息 |
| B、输出信息 |
| C、赋值，计算 |
| D、一个算法的起始和结束 |
下列关于独立性检验的说法中，错误的是（ ）
| A、独立性检验得到的结论一定正确 |
| B、独立性检验依赖小概率原理 |
| C、样本不同，独立性检验的结论可能有差异 |
| D、独立性检验不是判定两事物是否相关的唯一方法 |