题目内容
令P（x）：ax2+3x+2＞0，若对任意x∈R，P（x）是真命题，则实数a的取值范围是（ ）
| A、a＞0 | ||
B、a＞
| ||
| C、a＜0 | ||
| D、a=0 |
考点：全称命题
专题：函数的性质及应用,概率与统计
分析：将条件转化为ax2+3x+2＞0恒成立，检验a=0是否满足条件，当a≠0 时，必须
，从而解出实数a的取值范围．
|
解答：
解：对任意x∈R，P（x）：“ax2+3x+2＞0恒成立”是真命题，
当a=0 时，命题不成立，
当a≠0 时，要使命题是真命题成立，必须
，解得 a＞
，
故选：B．
当a=0 时，命题不成立，
当a≠0 时，要使命题是真命题成立，必须
|
| 9 |
| 8 |
故选：B．
点评：本题考查一元二次不等式的应用，注意联系对应的二次函数的图象特征，体现了等价转化和分类讨论的数学思想．
练习册系列答案
相关题目
圆（x-1）2+（y+2）2=20在x轴上截得的弦长是（ ）
| A、8 | ||
| B、6 | ||
C、6
| ||
D、4
|
把函数y=sin3x的图象适当变化就可以得到y=
（sin3x-cos3x）的图象，这个变化可以是（ ）
| ||
| 2 |
A、沿x轴方向向右平移
| ||
B、沿x轴方向向左平移
| ||
C、沿x轴方向向右平移
| ||
D、沿x轴方向向左平移
|
已知函数f（x）=|x+2|-|x-1|，则f（x）的值域是（ ）
| A、（-3，3） |
| B、[-3，3] |
| C、[3，+∞） |
| D、[-3，+∞） |
在演绎推理“因为平行四边形的对角线互相平分，而正方形是平行四边形，所以正方形的对角线互相平分．”中“正方形是平行四边形”是“三段论”的（ ）
| A、大前提 | B、小前提 |
| C、结论 | D、其它 |
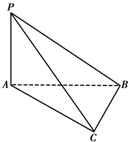如图所示，已知PA垂直于△ABC所在平面，且∠ACB=90°，连结PB、PC，则图形中互相垂直的平面有（ ）| A、一对 | B、两对 | C、三对 | D、四对 |
F1，F2分别是双曲线
-
=1（a＞0，b＞0）的左右焦点，以O为圆心，OF1为半径的圆与双曲线在第一象限的交点为P，若三角形PF1F2的面积为3a2，则双曲线离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
如图程序运行结果为（ ）
| A、3 | B、4 | C、5 | D、6 |