题目内容
正四棱锥的侧棱长为2
，侧棱与底面所成角为60°，则该四棱锥的高为 ．
| 3 |
考点：点、线、面间的距离计算,棱锥的结构特征
专题：空间位置关系与距离
分析：求出底面正四边形的对角线的长，然后求出边长，求出棱锥的高即可．
解答：
解：正四棱锥的侧棱长为2
，侧棱与底面所成的角为60°，
所以底面对角线的长为2×
×2
=2
，底面边长为
．
棱锥的高为2
×
=3．
故答案为：3．
| 3 |
所以底面对角线的长为2×
| 1 |
| 2 |
| 3 |
| 3 |
| 6 |
棱锥的高为2
| 3 |
| ||
| 2 |
故答案为：3．
点评：本题是基础题，考查棱长与底面所成的角，棱锥的高，底面边长的求法，考查计算能力，空间想象能力，常考题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
给定△ABC，若点D满足
=
，
=
+λ
，则λ等于（ ）
| AD |
| 2 |
| 3 |
| AB |
| CD |
| 1 |
| 3 |
| CA |
| CB |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
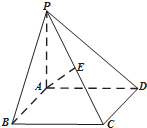如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，AB=2，AD=2