题目内容
解下列关于x的方程:
(1)2sinx+cosx=2;
(2)sin2x=sin2x;
(3)cosx+2=2tan2(
)
(1)2sinx+cosx=2;
(2)sin2x=sin2x;
(3)cosx+2=2tan2(
| x |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)结合同角三角函数基本关系式求解,结合换元法进行求解;
(2)利用分解因式,然后,结合三角函数值的范围进行求解即可;
(3)利用二倍角公式进行化简求解.
(2)利用分解因式,然后,结合三角函数值的范围进行求解即可;
(3)利用二倍角公式进行化简求解.
解答:
解:(1)∵2sinx+cosx=2
∴cosx=2(1-sinx),
∵sin2x+cos2x=1,
∴sin2x+4(1-sinx)2=1,
∴5sin2x-8sinx+3=0,
∴sinx=1或sinx=
,
当sinx=1时,x=
+2kπ,(k∈Z),
当sinx=
时,x=arcsin
+2kπ或x=π-arcsin
+2kπ(k∈Z),
∴方程的解为:x=
+2kπ或x=arcsin
+2kπ或x=π-arcsin
+2kπ(k∈Z);
(2)∵sin2x=sin2x
∴2sinxcosx=sin2x,
∴sinx(2cosx-sinx)=0,
∴sinx=0或2cosx-sinx=0,
当sinx=0时,x=kπ,(k∈Z),
当2cosx-sinx=0时,tanx=2,
∴x=arctan2+kπ,
∴方程的解为:x=kπ或x=arctan2+kπ,(k∈Z),
(3)∵cosx+2=2tan2(
),
∵tan2(
)=
,
∴cosx+2=2
,
∴cos2x+3cosx=0,
∴cosx(cosx+3)=0,
∵cosx+3≠0,
∴cosx=0.
∴x=
+kπ,k∈Z,
∴方程的解为:x=
+kπ,(k∈Z).
∴cosx=2(1-sinx),
∵sin2x+cos2x=1,
∴sin2x+4(1-sinx)2=1,
∴5sin2x-8sinx+3=0,
∴sinx=1或sinx=
| 3 |
| 5 |
当sinx=1时,x=
| π |
| 2 |
当sinx=
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
∴方程的解为:x=
| π |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
(2)∵sin2x=sin2x
∴2sinxcosx=sin2x,
∴sinx(2cosx-sinx)=0,
∴sinx=0或2cosx-sinx=0,
当sinx=0时,x=kπ,(k∈Z),
当2cosx-sinx=0时,tanx=2,
∴x=arctan2+kπ,
∴方程的解为:x=kπ或x=arctan2+kπ,(k∈Z),
(3)∵cosx+2=2tan2(
| x |
| 2 |
∵tan2(
| x |
| 2 |
| 1-cosx |
| 1+cosx |
∴cosx+2=2
| 1-cosx |
| 1+cosx |
∴cos2x+3cosx=0,
∴cosx(cosx+3)=0,
∵cosx+3≠0,
∴cosx=0.
∴x=
| π |
| 2 |
∴方程的解为:x=
| π |
| 2 |
点评:本题综合考查了三角函数基本关系式,三角公式等知识,二倍角公式及其运用等综合题目,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X<2)=( )
| A、0.1588 |
| B、0.1587 |
| C、0.1586 |
| D、0.1585 |
已知某几何体的三视图如图所示,则该几何体的体积为( )
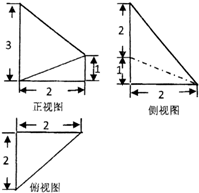

| A、8 | ||
B、
| ||
| C、4 | ||
| D、12 |
 学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?
学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?