题目内容
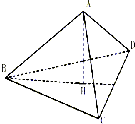已知正三棱锥A-BCD的侧面积为3| 6 |
| 2 |
考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：根据几何体的性质，求解出底面边长，三棱锥的高，运用体积公式求解．
解答：
解：设CD中点为O，连接OA，底面边长为a
∴0A=
，
∵正三棱锥A-BCD的侧面积为3
cm2
∴a=2
，即正三角形中心到边的距离为1
∵侧面ACD底边CD上的高为
cm
∴正三棱锥A-BCD为h=
=1
∴正三棱锥A-BCD的体积=
×（
×（2
）2）×1=
，
故答案为：
设CD中点为O，连接OA，底面边长为a∴0A=
| 3 |
∵正三棱锥A-BCD的侧面积为3
| 6 |
∴a=2
| 3 |
∵侧面ACD底边CD上的高为
| 2 |
∴正三棱锥A-BCD为h=
| 2-1 |
∴正三棱锥A-BCD的体积=
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 3 |
故答案为：
| 3 |
点评：本题考察了空间几何体的性质，运用体积公式求解，属于中档题．
练习册系列答案
相关题目
如图，E、F分别是三棱锥P-ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（ ）| A、30° | B、60° |
| C、0° | D、120° |
在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A（1，2）其焦点F在x轴上．如果双曲线的a=2，一个焦点为（5，0），则其标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|