Question

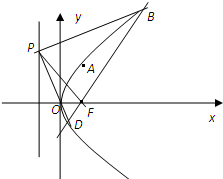在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A（1，2）其焦点F在x轴上．
（Ⅰ）求抛物线C的标准方程；
（Ⅱ）求过点F和OA的中点的直线的方程；
（Ⅲ）设点P（-1，m），过点F的直线交抛物线C于B、D两点，记PB，PF，PD的斜率分别为k₁，k₂，k₃，求证：k₁+k₃=2k₂．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（Ⅰ）由题意可设抛物线的方程为：y²=2px，（p＞0），由已知得4=2p，由此能求出抛物线C的标准方程．
（Ⅱ）由（1）知：F（1，0），OA的中点M的坐标为（

1

2

，1），由此能求出直线FM的方程．
（Ⅲ）当直线的斜率不存在时，F（1，0），B（1，2），D（1，-2），k₁+k₃=2k₂；当直线的斜率存在时，设直线的方程为y=k（x-1），设B（x₁，y₁），D（x₂，y₂），由已知条件推导出k1+k3=2k-(2k+m)(

1

x1+1

+

1

x2+1

)
=2k-（2k+m）-

x1+x2+2

x1x2+x1+x2+1

，由此能证明k₁+k₃=2k₂．

解答： （Ⅰ）解：由题意可设抛物线的方程为：y²=2px，（p＞0），
因为抛物线经过点A（1，2），所以4=2p，解得：p=2，
则抛物线C的标准方程是：y²=4x．…（3分）
（Ⅱ）解：由（1）知：F（1，0），OA的中点M的坐标为（

1

2

，1），
则k_FM=

1-0

1 2 -1

=-2，
所以直线FM的方程是：2x+y-2=0．…（6分）
（Ⅲ）证明：当直 线的斜率不存在时，则F（1，0），B（1，2），D（1，-2），
所以k1=

2-m

2

，k2=-

m

2

，k3=

-2-m

2

，
则k₁+k₃=2k₂，…（8分）
当直线的斜率存在时，设为k，则直线的方程为y=k（x-1），
设B（x₁，y₁），D（x₂，y₂），
则k1=

y1-m

x1+1

=

k(x1-1)-m

x1+1

=k-

2k+m

x1+1

，
同理可得：k3=k-

2k+m

x2+1

，
所以k1+k3=2k-(2k+m)(

1

x1+1

+

1

x2+1

)
=2k-（2k+m）-

x1+x2+2

x1x2+x1+x2+1

，…（12分）
由方程组

x2 4 + y2 16 =1 y=k(x-1)

，消去y，并整理得：k²x²-2（k²+2）x+k²=0，
所以x₁x₂=1，…（14分）
则k₁+k₃=2k-（2k+m）×1=-m，
又k2=-

m

2

，所以k₁+k₃=2k₂，
综上所述：k₁+k₃=2k₂．…（16分）

点评：本题考查抛物线C的标准方程的求法，考查直线的方程的求法，考查k₁+k₃=2k₂的证明，解题时要认真审题，注意函数与方程思想的合理运用．