题目内容
已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数g(x)=
+f(x)在[1,2]上是减函数,求实数a的取值范围.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数g(x)=
| 2 |
| x |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由导数的几何意义得f'(2)=1,解得即可;
(2)根据函数的单调性与导数的关系可得g'(x)≤0在[1,2]上恒成立,即-
+2x+
≤0在[1,2]上恒成立.即a≤
-x2在[1,2]上恒成立.利用导数求出函数h(x)=
-x2,在[1,2]上的最小值,即可得出结论.
(2)根据函数的单调性与导数的关系可得g'(x)≤0在[1,2]上恒成立,即-
| 2 |
| x2 |
| 2a |
| x |
| 1 |
| x |
| 1 |
| x |
解答:
解:(1)f′(x)=2x+
=
…(2分)
由已知f'(2)=1,解得a=-3.…(4分)
(2)由g(x)=
+x2+2alnx得g′(x)=-
+2x+
,
由已知函数g(x)为[1,2]上的单调减函数,
则g'(x)≤0在[1,2]上恒成立,
即-
+2x+
≤0在[1,2]上恒成立.
即a≤
-x2在[1,2]上恒成立.…(9分)
令h(x)=
-x2,在[1,2]上h′(x)=-
-2x=-(
+2x)<0,
所以h(x)在[1,2]为减函数.h(x) min=h(2)=-
,
所以a≤-
.…(13分)
| 2a |
| x |
| 2x2+2a |
| x |
由已知f'(2)=1,解得a=-3.…(4分)
(2)由g(x)=
| 2 |
| x |
| 2 |
| x2 |
| 2a |
| x |
由已知函数g(x)为[1,2]上的单调减函数,
则g'(x)≤0在[1,2]上恒成立,
即-
| 2 |
| x2 |
| 2a |
| x |
即a≤
| 1 |
| x |
令h(x)=
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x2 |
所以h(x)在[1,2]为减函数.h(x) min=h(2)=-
| 7 |
| 2 |
所以a≤-
| 7 |
| 2 |
点评:本题主要考查导数的几何意义,利用导数研究函数的单调性、最值等知识,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知函数f(x)=x2+ex-
(x<0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范围是( )
| 1 |
| 2 |
A、(-∞,
| ||||||
B、(-∞,
| ||||||
C、(-
| ||||||
D、(-
|
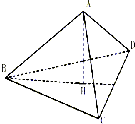 已知正三棱锥A-BCD的侧面积为3
已知正三棱锥A-BCD的侧面积为3