题目内容
9.已知${({x+a})^2}{({2x-\frac{1}{x}})^5}$的展开式中不含x3的项,则a=±1.分析 先求得二项式展开式的通项公式,求得含x3项的系数,于是可是得到关于a的方程解得即可.
解答 解:${({x+a})^2}{({2x-\frac{1}{x}})^5}$=x2(2x-$\frac{1}{x}$)5+2ax(2x-$\frac{1}{x}$)5+a2(2x-$\frac{1}{x}$)5,其中含x3的项的系数为:${2}^{3}{C}_{5}^{2}-{2}^{4}{a}^{2}{C}_{5}^{1}$=80-80a2=0,所以a=±1.
故答案为:±1.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,二项式系数的性质,属基础题.

练习册系列答案
相关题目
19.已知f(x)是定义在实数集R上的不恒为零的偶函数,且xf(x+1)=(x+1)f(x)对任意实数x恒成立,则$f[f(\frac{5}{2})]$的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
19.数列{an}中,已知对任意自然数n,a1+a2+a3+…+an=2n,则a12+a22+a32+…+an2=( )
| A. | $\frac{1}{3}$(4n-1) | B. | $\frac{1}{3}$(2n-1) | C. | 4n-1 | D. | $\frac{1}{3}$(4n+8) |
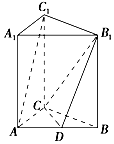 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.