题目内容
已知一圆的方程式为x2+y2=v2t2,将该圆向下移动
gt2个单位,求移动后圆的方程.
| 1 |
| 2 |
考点:圆的一般方程
专题:直线与圆
分析:直接利用图象平移原则,推出圆的方程即可.
解答:
解:圆的方程式为x2+y2=v2t2,将该圆向下移动
gt2个单位,
可得:(x-
gt2)2+y2=v2t2,
移动后圆的方程:(x-
gt2)2+y2=v2t2.
| 1 |
| 2 |
可得:(x-
| 1 |
| 2 |
移动后圆的方程:(x-
| 1 |
| 2 |
点评:本题考查图象的平移变换,圆的方程的求法,考查计算能力.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知直线l:y=x+m(m∈R),若以点M(2,0)为圆心的圆与直线l相切于点P,且P在y轴上,则该圆的方程为( )
| A、(x-2)2+y2=8 |
| B、(x+2)2+y2=8 |
| C、x2+(y-2)2=8 |
| D、x2+(y+2)2=8 |
不同三点A,B,C满足(
•
):(
•
):(
•
)=3:4:5,则这三点( )
| BC |
| CA |
| CA |
| AB |
| AB |
| BC |
| A、组成锐角三角形 |
| B、组成直角三角形 |
| C、组成钝角三角形 |
| D、在同一条直线上 |
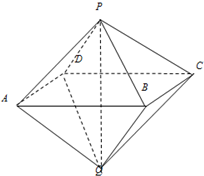 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高都是2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高都是2,AB=4. 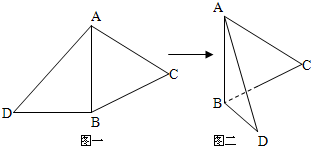 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中.
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中.