题目内容
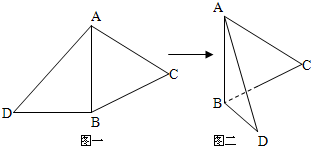 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中.
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中.(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD所成的角的正弦值.
考点:直线与平面所成的角,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明BD⊥面ABC,即可证明BD⊥AC;
(2)依题意建立空间直角坐标系使得△ABC在yoz平面上,由已知条件分别求出点C和点D的空间坐标,利用空间两点间的距离公式能求出D、C之间的距离.
(3)由题设取AB的中点H,连结CH、DH和DC,证明∠CDH为直线DC与面ABD所成的角,即可求出CD与平面ABD所成的角.
(2)依题意建立空间直角坐标系使得△ABC在yoz平面上,由已知条件分别求出点C和点D的空间坐标,利用空间两点间的距离公式能求出D、C之间的距离.
(3)由题设取AB的中点H,连结CH、DH和DC,证明∠CDH为直线DC与面ABD所成的角,即可求出CD与平面ABD所成的角.
解答:
(1)证明:∵面ABD⊥面ABC,面ABD∩面ABC=AB,BD?面ABD,BD⊥AB,
∴BD⊥面ABC,
又∵AC?面ABC,∴BD⊥AC…(4分)
(2)解:∵BD⊥面ABC,BC?面ABC,
∴BD⊥BC
在Rt△DBC中,BC=BA=2,BD=2,∴DC=
=
=2
…(8分)
(3)解:取AB的中点H,连结CH、DH和DC,则
∵△ABC是正三角形,∴CH⊥AB,
又∵面ABD⊥面ABC,∴CH⊥面ABD,即DH是DC在面ABD内的射影
则∠CDH为直线DC与面ABD所成的角 …(10分)
∵CH=
BC=
,DC=2
,
∴sin∠CDH=
=
故直线DC与面ABD所成的角的正弦值为
.…(12分)
∴BD⊥面ABC,
又∵AC?面ABC,∴BD⊥AC…(4分)
(2)解:∵BD⊥面ABC,BC?面ABC,
∴BD⊥BC
在Rt△DBC中,BC=BA=2,BD=2,∴DC=
| DB2+BC2 |
| 22+22 |
| 2 |
(3)解:取AB的中点H,连结CH、DH和DC,则
∵△ABC是正三角形,∴CH⊥AB,
又∵面ABD⊥面ABC,∴CH⊥面ABD,即DH是DC在面ABD内的射影
则∠CDH为直线DC与面ABD所成的角 …(10分)
∵CH=
| ||
| 2 |
| 3 |
| 2 |
∴sin∠CDH=
| CH |
| DC |
| ||
| 4 |
故直线DC与面ABD所成的角的正弦值为
| ||
| 4 |
点评:本题考查线面垂直的证明,考查空间两点间的距离的求法,考查直线与平面所成角的大小的求法,正确运用线面垂直的判定定理是关键.

练习册系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的一条渐近方程为y=
x,则C的离心率为( )
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
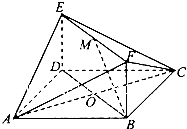 如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=
如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=