题目内容
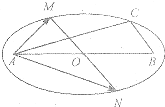在△ABC中，CA=3CB，cosC=-| 1 |
| 3 |
（Ⅰ）求椭圆的离心率e；
（Ⅱ）若AB=2
| 3 |
| AM |
| AN |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）设|CB|=t，则|CA|=3t，由余弦定理，得|AB|=2
t，由此能求出离心率e．
（Ⅱ）由e=
，|AB|=2
，知c=
，a=2，b=1，以A，B所在直线为x轴，AB中点O为原点，建立平面直角坐标系，由此能求出x0=0时，
•
有最大值2．
| 3 |
（Ⅱ）由e=
| ||
| 2 |
| 3 |
| 3 |
| AM |
| AN |
解答：
解：（Ⅰ）设|CB|=t，则|CA|=3t，
由余弦定理，得AB2=CB2+CA2-2CA•CB•cosC=12t2，
∴|AB|=2
t，
∵以A，B为焦点的椭圆E经过点C，
∴由椭圆定义知2a=|CB|+|CA|=4t，则a=2t，
又|AB|=2c，则c=
t，
∴离心率e=
=
．
（Ⅱ）由（Ⅰ）e=
，∵|AB|=2
，
∴c=
，∴a=2，b=1，
以A，B所在直线为x轴，AB中点O为原点，
建立平面直角坐标系如图所示，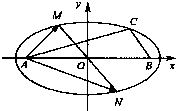
则对应的椭圆的标准方程为
+y2=1，A（-
，0），
依题意设M（x0，y0），N（-x0，y0），
∴
=(x0+
，y0)，
=(-x0+
，-y0)，
∴
•
=(x0+
)(-x0+
)+y0（-y0）=-x02+3-y02，
∵
+y02=1，
∴-x02+3-y02=-x02+3-(1-
)=-
x02+2，
又∵-2≤x0≤2，∴x0=0时，
•
有最大值2．
由余弦定理，得AB2=CB2+CA2-2CA•CB•cosC=12t2，
∴|AB|=2
| 3 |
∵以A，B为焦点的椭圆E经过点C，
∴由椭圆定义知2a=|CB|+|CA|=4t，则a=2t，
又|AB|=2c，则c=
| 3 |
∴离心率e=
| c |
| a |
| ||
| 2 |
（Ⅱ）由（Ⅰ）e=
| ||
| 2 |
| 3 |
∴c=
| 3 |
以A，B所在直线为x轴，AB中点O为原点，
建立平面直角坐标系如图所示，
则对应的椭圆的标准方程为
| x2 |
| 4 |
| 3 |
依题意设M（x0，y0），N（-x0，y0），
∴
| AM |
| 3 |
| AN |
| 3 |
∴
| AM |
| AN |
| 3 |
| 3 |
∵
| x02 |
| 4 |
∴-x02+3-y02=-x02+3-(1-
| x02 |
| 4 |
| 3 |
| 4 |
又∵-2≤x0≤2，∴x0=0时，
| AM |
| AN |
点评：本题考查椭圆离心率的求法，考查向量数量积最大值的求法，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
相关题目
袋中有大小相同的2个红球，4个白球，从袋中有放回地依次摸取2球，则两次均取出白球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
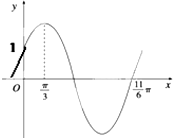已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜
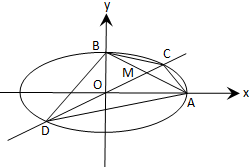如图所示，已知A，B分别是椭圆E：