题目内容
设f（x）=
（a，b为常数）
（1）若a=b=1时，求证：f（x）不是奇函数；
（2）若a=1，b=2时，求证：f（x）是奇函数；
（3）若a=-1，b=-2时，解不等式f（x）≤3．
| -2x+a |
| 2x+1+b |
（1）若a=b=1时，求证：f（x）不是奇函数；
（2）若a=1，b=2时，求证：f（x）是奇函数；
（3）若a=-1，b=-2时，解不等式f（x）≤3．
考点：函数奇偶性的判断,函数奇偶性的性质
专题：函数的性质及应用
分析：（1）若a=b=1时，求出函数的表达式，利用函数奇偶性的定义即可判断f（x）不是奇函数；
（2）若a=1，b=2时，求出函数的表达式，利用函数奇偶性的定义即可判断f（x）是奇函数；
（3）若a=-1，b=-2时，求出函数的表达式，利用指数函数的性质即可判断解不等式．
（2）若a=1，b=2时，求出函数的表达式，利用函数奇偶性的定义即可判断f（x）是奇函数；
（3）若a=-1，b=-2时，求出函数的表达式，利用指数函数的性质即可判断解不等式．
解答：
解：（1）若a=b=1时，则f（x）=
=
，
则f（1）=
=-
，f（-1）=
=
，
∵f（-1）≠-f（1），
∴f（x）不是奇函数；
（2）若a=1，b=2时，f（x）=
=
，
∵f（-x）=
=
=
=-f（x），
∴f（x）是奇函数；
（3）若a=-1，b=-2时，f（x）=
=
=-
+
，（x≠0）
则f（x）在（-∞，0）和（0，+∞）上为增函数．
①当x＞0，则2x＞1，f（x）＜-
＜3，
②当x＜0，则2x＜1，f（x）＞-
，
则由-
+
≤3，解得x≤log2
，
∴f（x）≤3的解集为（-∞，log2
]∪（0，+∞）．
| -2x+a |
| 2x+1+b |
| -2x+1 |
| 2x+1+1 |
则f（1）=
| -2+1 |
| 22+1 |
| 1 |
| 5 |
| -2-1+1 |
| 2-1+1+1 |
| 1 |
| 4 |
∵f（-1）≠-f（1），
∴f（x）不是奇函数；
（2）若a=1，b=2时，f（x）=
| -2x+a |
| 2x+1+b |
| -2x+1 |
| 2x+1+2 |
∵f（-x）=
| -2-x+1 |
| 2-x+1+2 |
-
| ||
|
| 2x-1 |
| 2x+1+2 |
∴f（x）是奇函数；
（3）若a=-1，b=-2时，f（x）=
| -2x+a |
| 2x+1+b |
| -2x-1 |
| 2x+1-2 |
| 1 |
| 2 |
| 1 |
| 1-2x |
则f（x）在（-∞，0）和（0，+∞）上为增函数．
①当x＞0，则2x＞1，f（x）＜-
| 1 |
| 2 |
②当x＜0，则2x＜1，f（x）＞-
| 1 |
| 2 |
则由-
| 1 |
| 2 |
| 1 |
| 1-2x |
| 5 |
| 7 |
∴f（x）≤3的解集为（-∞，log2
| 5 |
| 7 |
点评：本题主要考查函数奇偶性的判断，以及不等式的求解，根据定义法是解决本题的关键．
练习册系列答案
相关题目
下列命题为真命题的是（ ）
| A、?x∈R，sinx＞2 |
| B、?x∈R，x2≥0 |
| C、所有的等腰三角形都是等边三角形 |
| D、所有的平行向量都相等 |
已知sinα=-
，则sin（π+α）=（ ）
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
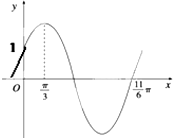已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜