题目内容

已知函数f（x）=sin（x+
π
12
）．
（1）求f（-
π
4
）的值；
（2）若cosθ=
4
5
，θ∈（0，
π
2
），求f（2θ-
π
3
）．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：（1）把x=-
π
4
代入函数解析式即可．
（2）根据函数解析式求得f（2θ-
π
3
）的表达式并利用两角和公式整理，根据cosθ的值，求得sinθ的值，进而根据二倍角公式分别求得sin2θ和cos2θ的值，代入f（2θ-
π
3
）的解析式．
解答： 解：（1）f（-
π
4
）=sin（-
π
4
+
π
12
）=sin（-
π
6
）=-
1
2
．
（2）f（2θ-
π
3
）=sin（2θ-
π
3
+
π
12
）=sin（2θ-
π
4
）=
2
2
（sin2θ-cos2θ），
因为cosθ=
4
5
，θ∈（0，
π
2
），所以sinθ=
3
5
，
所以sin2θ=2sinθcosθ=
24
25
，cos2θ=cos2θ-sin2θ=
7
25
，
所以f（2θ-
π
3
）=
2
2
（sin2θ-cos2θ）=（
24
25
-
7
25
）×
2
2
=
17
2
50
．
点评：本题主要考查了两角和公式和二倍角公式的应用．考查了学生对基础知识的灵活运用．
练习册系列答案
相关题目
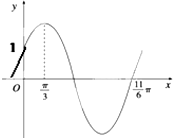已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜
π
2
）的部分图象如图．
（Ⅰ）求f（x）的解析式；
（Ⅱ）将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的
1
2
倍，再将所得函数图象向右平移
π
6
个单位，得到函数y=g（x）的图象，求g（x）的单调递增区间．
设命题p：指数函数y=（m2-5m+7）x在R上单调递增；命题q：y=lg（x2+2mx+m）的定义域为R，若“p∨q”为真命题，若“p∧q”为假命题．求实数m的取值范围．
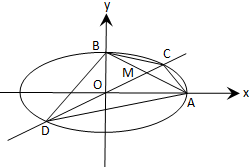如图所示，已知A，B分别是椭圆E：
x2
a2
+
y2
b2
=1，（a＞b＞0）的右顶点和上顶点，|OA|=2，点M为线段AB中点，直线OM交椭圆于C，D两点（其中O为坐标原点），△ABC与△ABD的面积分别记为S1，S2．
（1）当椭圆E的离心率e=
1
2
时，求椭圆E的方程；
（2）当椭圆E的离心率变变化时，
S1
S2
是否为定值？若是求出该定值，若不是说明理由．
已知F1，F2为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点，过F2做椭圆的弦AB，若△AF1B 的周长是16，椭圆的离心率e=
3
2
．
（1）求椭圆的标准方程；       
（2）若∠F1AF2=90°，求△F1AF的面积S；
（3）已知P（2，1）是椭圆内一点，在椭圆上求一点Q，使得
3
PQ+2QF2最小，并求出最小值．
已知cos（π+α）=
4
5
，α为第三象限角．
（1）求sinα，tanα的值；
（2）求sin（α+
π
4
），tan2α的值．
已知函数g（x）=（2-a）lnx，h（x）=lnx+ax2（a∈R），令f（x）=g（x）+h′（x）
（Ⅰ）当a=1时，求函数y=
x
g(x)
的图象上斜率为-2的切线方程；
（Ⅱ）当a＜-2时，求f（x）的单调区间；
（Ⅲ）当-3＜a＜-2时，若存在λ1，λ2∈[1，3]，使得|f（λ1）-f（λ2）|＞（m+ln3）a-2ln3成立，求m的取值范围．
已知函数f（x）=[x]+|sin
πx
2
|，x∈[-1，1]．其中[x]表示不超过x的最大整数，例如[-3.5]=-4，[2.1]=2．
（Ⅰ）试判断函数f（x）的奇偶性，并说明理由；
（Ⅱ）求函数f（x）的值域．
已知x＞0，y＞0，且
2
x
+
1
y
=4，则x+2y最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网