题目内容
一直异面直线a,b分别在α,β内,面α∩β=c,则直线c( )
| A、一定与a,b中的两条都相交 |
| B、至少与a,b中的一条平行 |
| C、至多与a,b中的一条相交 |
| D、至少与a,b中的一条相交 |
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:根据平行公理,异面直线判定,逐项进行判断,进而得到答案.
解答:
解:对于A:若直线c与a,b中的一条相交,另一条平行也可以,故A错误;
对于B:c与a,b都平行,得出a,b平行,与a,b异面矛盾,故B错误;
对于C:c可以和a,b都相交,故C错误;
对于D:如果c与a,b均不相交,则直线c与a,b均平行,与已知矛盾,故D正确;
故选D
对于B:c与a,b都平行,得出a,b平行,与a,b异面矛盾,故B错误;
对于C:c可以和a,b都相交,故C错误;
对于D:如果c与a,b均不相交,则直线c与a,b均平行,与已知矛盾,故D正确;
故选D
点评:本题考查的知识点是空间中直线与直线之间的位置关系,其中熟练掌握空间直线不同位置关系的定义及几何特征是解答本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
已知点A(l,2)在函数f(x)=ax3的图象上,则过点A的曲线C:y=f(x)的切线方程是( )
| A、6x-y-4=0 |
| B、x-4y+7=0 |
| C、6x-y-4=0或x-4y+7=0 |
| D、6x-y-4=0或3x-2y+1=0 |
记f(n)为自然数n的个位数字,an=f(n2)-f(n).则a1+a2+a3+…+a2016的值为( )
| A、2 | B、6 | C、8 | D、10 |
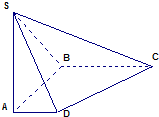 在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<
在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<