题目内容
已知锐角α,β满足sinα=
,cosβ=
,则α+β=( )
| ||
| 5 |
3
| ||
| 10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:两角和与差的余弦函数,两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:由α、β∈(0,
),利用同角三角函数的关系算出cosα、sinβ的值,进而根据两角和的余弦公式算出cos(α+β)=
,结合α+β∈(0,π)可得α+β的值.
| π |
| 2 |
| ||
| 2 |
解答:
解:∵α、β∈(0,
),满足sinα=
,cosβ=
,
∴cosα=
=
,sinβ=
=
.
由此可得cos(α+β)=cosαcosβ-sinαsinβ=
•
-
•
=
.
又∵α+β∈(0,π),∴α+β=
.
故选:A.
| π |
| 2 |
| ||
| 5 |
3
| ||
| 10 |
∴cosα=
| 1-sin2α |
2
| ||
| 5 |
| 1-cos2β |
| ||
| 10 |
由此可得cos(α+β)=cosαcosβ-sinαsinβ=
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 5 |
| ||
| 2 |
又∵α+β∈(0,π),∴α+β=
| π |
| 4 |
故选:A.
点评:本题给出角α、β满足的条件,求α+β的值.着重考查了特殊角的三角函数值、同角三角函数的基本关系、两角和的余弦公式等知识,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知a,b∈R,且ab≠0,则在下列四个不等式中,不恒成立的是( )
A、
| ||||
B、
| ||||
C、ab≤(
| ||||
D、(
|
记f(n)为自然数n的个位数字,an=f(n2)-f(n).则a1+a2+a3+…+a2016的值为( )
| A、2 | B、6 | C、8 | D、10 |
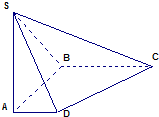 在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<
在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<