题目内容
已知全集U=R,集合A={y|y=x2-
x+1,x∈[0,2]},B={x|y=
},求集合A,B,(∁UA)∪B.
| 3 |
| 2 |
| 1-x2 |
考点:交、并、补集的混合运算
专题:集合
分析:根据函数的图象和性质,求出集合A={y|y=x2-
x+1,x∈[0,2]},B={x|y=
},进而结合集合交集,并集,补集的定义,可得答案.
| 3 |
| 2 |
| 1-x2 |
解答:
解:A={y|y=x2-
x+1,x∈[0,2]}
={y|y=(x-
)2+
,x∈[0,2]}={y|
≤y≤2},…(4分)
B={x|y=
}={x|1-x2≥0}={x|-1≤x≤1}…(8分)
∴∁UA={y|y>2或y<
},…(10分)
(∁UA)∪B={x|x≤1或x>2}…(12分)
| 3 |
| 2 |
={y|y=(x-
| 3 |
| 4 |
| 7 |
| 16 |
| 7 |
| 16 |
B={x|y=
| 1-x2 |
∴∁UA={y|y>2或y<
| 7 |
| 16 |
(∁UA)∪B={x|x≤1或x>2}…(12分)
点评:本题考查的知识点是集合的交集,并集,补集及其运算,难度不大,属于基础题.

练习册系列答案
相关题目
已知偶函数f(x)在[0,+∞)单调递减,A(2,1)的其图象上.那么f(x+1)>1的解集为( )
| A、(-2,2) |
| B、(-3,1) |
| C、[0,2) |
| D、(-1,3) |
已知点A(l,2)在函数f(x)=ax3的图象上,则过点A的曲线C:y=f(x)的切线方程是( )
| A、6x-y-4=0 |
| B、x-4y+7=0 |
| C、6x-y-4=0或x-4y+7=0 |
| D、6x-y-4=0或3x-2y+1=0 |
在△ABC中,角A,B,C的对边分别是a,b,c,若∠A:∠B=1:2,a:b=2:3,则cos2A的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
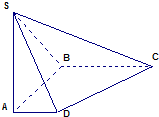 在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<
在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<