题目内容
设f（x）是R上的奇函数，当x≤0时，f（x）=2x2-x，则x＞0时，f（x）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：设x＞0，-x＜0，所以根据x≤0时的解析式便可求出f（-x），再根据f（x）是R上的奇函数便得到f（-x）=-f（x），这样即可求出x＞0时的f（x）解析式．
解答：
解：设x＞0，则-x＜0，由已知条件得：
f（-x）=2x2+x=-f（x）；
∴f（x）=-2x2-x．
故答案为：-2x2-x．
f（-x）=2x2+x=-f（x）；
∴f（x）=-2x2-x．
故答案为：-2x2-x．
点评：考查奇函数的定义，根据奇函数的定义求解析式．
练习册系列答案
阅读快车系列答案
相关题目
已知直线l：x+
y-3=0，该直线的倾斜角为（ ）
| 3 |
| A、150° | B、120° |
| C、60° | D、30° |
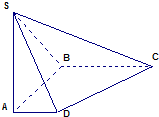在四棱锥S-ABCD中，SA⊥底面ABCD，AD⊥AB，AD∥BC，AD=1，AB=BC=2，cos＜