题目内容
13．已知（-1，y1），（-2，y2），（-4，y3）是抛物线y=-2x2-8x+m上的点，则（ ）| A． | y1＜y2＜y3 | B． | y3＜y2＜y1 | C． | y3＜y1＜y2 | D． | y2＜y3＜y1 |
分析 抛物线y=-2x2-8x+m开口朝下，且以直线x=-2为对称轴，进而可得三个函数值的大小．
解答 解：抛物线y=-2x2-8x+m开口朝下，且以直线x=-2为对称轴，
故f（-2）＞f（-1）=f（-3）＞f（-4），
即y3＜y1＜y2，
故选：C
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质是解答的关键．
练习册系列答案
相关题目
1．已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1，F2，过F1的直线l交椭圆与两点A，B，则|AF2|+|BF2|的最大值为（ ）
| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
8．正项等比数列{an}中，a6=a5+2a4，若存在两项am，an使得$\sqrt{{a_m}{a_n}}$=4a1，则$\frac{1}{m}$+$\frac{2}{n}$的最小值是（ ）
| A． | $\frac{{3+2\sqrt{2}}}{6}$ | B． | 1 | C． | $\frac{11}{5}$ | D． | $\frac{5}{4}$ |
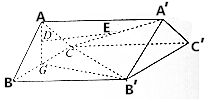已知正三棱柱ABC-A′B′C′如图所示，其中G是BC的中点，D，E分别在线段AG，A′C上运动，使得DE∥平面BCC′B′，CC′=2BC=4．
如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′=6，O′C′=2，则原图形OABC的面积为24$\sqrt{2}$．