题目内容
已知函数f（x）=
-
-
+
，问函数f（x4）是否存在零点，如果存在，求出零点，如果不存在，请说明理由．
| x+3 |
| x+2 |
| x+1 |
| x |
考点：函数的零点
专题：函数的性质及应用
分析：先说明函数f（x）=
-
-
+
不存在零点，进而可得函数f（x4）是不存在零点．
| x+3 |
| x+2 |
| x+1 |
| x |
解答：
解：函数f（x4）是不存在零点，理由如下：
∵f（x）=
-
-
+
=（
+
）-（
+
），
∴若f（x）=0，则（
+
）=（
+
），
即（
+
）2=（
+
）2，
即2x+3+2
=2x+3+2
，
即
=
，
∵
=
无解，
故函数f（x）没有零点，
故函数f（x4）是不存在零点．
∵f（x）=
| x+3 |
| x+2 |
| x+1 |
| x |
| x+3 |
| x |
| x+2 |
| x+1 |
∴若f（x）=0，则（
| x+3 |
| x |
| x+2 |
| x+1 |
即（
| x+3 |
| x |
| x+2 |
| x+1 |
即2x+3+2
| x2+3x |
| x2+3x+2 |
即
| x2+3x |
| x2+3+2 |
∵
| x2+3x |
| x2+3+2 |
故函数f（x）没有零点，
故函数f（x4）是不存在零点．
点评：本题考查的知识点是函数零点的存在性及个数判断，难度不大，属于基础题．
练习册系列答案
相关题目
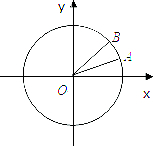如图，在平面直角坐标系中xOy中，以轴Ox为始边做两个锐角α，β，它们的终边分别与单位圆相交于A．B两点，已知A，B的纵坐标分别为
对某高中男子体育小组的50米跑成绩（单位：s）进行统计分析，得到如下的茎叶图（其中，茎表示成绩的整数部分，叶表示成绩的小数部分）；